| |
|
Hoofdstuk 15 - Kans verwachting
|
|
|
| Er zijn leugens, pertinente leugens en statistieken', luidt een bekende uitspraak. En onlangs kopte een Londense krant: 'Er is maar één ding erger dan het Engelse weer: het Engelse weerbericht.' Met deze beide zinsneden in gedachten lijkt een combinatie van het 'misbakselduo' statistiek en weervoorspelling bij voorbaat kansloos. Toch worden kansverwachtingen in de meteorologie al lange tijd toegepast. En met succes. |
| |
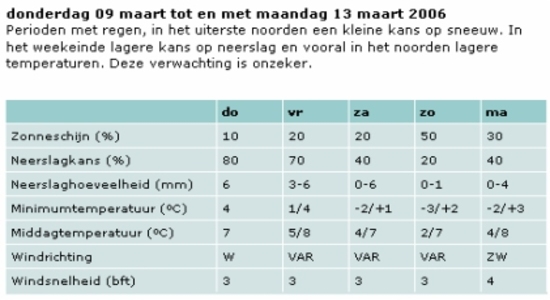
Weersverwachtingen geven aan wat het
weer gaat doen. Komt er wel of geen
regen? Hoe hoog loopt de temperatuur
op? Komt er mist? Hoe hard gaat het
waaien? De uitspraken of
beweringen die gedaan worden, gelden
voor een welomschreven tijdvak,
bijvoorbeeld vandaag, morgen of
overmorgen. Ze worden gemaakt voor
een aangegeven plaats, veelal een
luchthaven, of een bepaald gebied:
Nederland, Friesland, de Ardennen.
En ze komen uit of slaan de plank
mis. Want het regent of het blijft
droog, de temperatuur komt wel of
niet onder nul, de mist treedt op of
blijft uit
en de ondergrens voor windkracht 8
wordt bereikt of niet gehaald.
Verwachtingen met dergelijke
vastomlijnde uitspraken heten
deterministisch;
er wordt als het ware in 'bepaald'
hoe het weer zich zal ontwikkelen
(vergelijk figuur 1). Deze manier
van benaderen is niet altijd handig.
Neem een weersituatie waarin zich
gewoonlijk buien voordoen. |
| |
De meteoroloog die de verwachting
voor die dag opstelt, is er zeker
van dat er buien komen. Op welke
plek in Nederland of België de buien
zich zullen voordoen en of dat nog
gebeurt in de
periode waarvoor de
verwachting geldt of direct daarna,
is echter onzeker. Een voorspelling
met
alleen 'droog' of alleen 'regen'
erin zal onder dergelijke
omstandigheden geregeld mislukken.
Vooroordelen over de kwaliteit van
de weersverwachting worden op die
manier wel erg gemakkelijk gevoed.
De terministische verwachtingen
leiden ook tot teleurstellingen in
gevallen waarbij de scheidingslijn
tussen warme, uit de omgeving van de
Azoren afkomstige lucht, en koudere
lucht van het noordelijk deel van de
Atlantische Oceaan gedurende langere
tijd over of dicht bij
Nederland
ligt. Zo'n situatie kan dagenlang
aanhouden, wat de verwachting voor
morgen, overmorgen en de dagen
daarna behoorlijk lastig maakt. Hoe
verder vooruit, des te onzekerder is
doorgaans de ligging van het front,
zoals zo'n scheidingslijn wordt
genoemd.
De onzekerheidsmarges zijn vaak veel
groter dan de afstand tussen de
Noordzeekust en de Duitse grens.Als
de meteoroloog dan een temperatuur
moet noemen of moet aangeven of het
al dan niet zal regenen, is hij of
zij niet te beroerd om
dat te doen.
Maar daarmee wordt aan
de
beschikbare informatie geen recht
gedaan. |
| |
 |
|
 |
| |
In tekstverwachtingen kan iets van
die onzekerheid worden vermeld: Hier
en daar een bui, enkele mistbanken,
plaatselijk vorst aan de grond,
mogelijk storm. Of in een
uitgebreider weerpraatje: daarna
onzeker, de computermodellen spreken
elkaar tegen. 'Ze weten het niet',
denkt de gebruiker dan. Of: 'De
meteoroloog dekt zich in tegen
fouten; een typisch staaltje van
defensieve meteorologie'. 'Wij
leveren de afnemers extra
informatie', motiveert de
meteoroloog de gekozen formulering
vanuit zijn zekerheid over de
onzekerheden die de weersituatie op
dat moment met ltje van
defensieve meteorologie'. 'Wij
leveren de afnemers extra
informatie', motiveert de
meteoroloog de gekozen formulering
vanuit zijn zekerheid over de
onzekerheden die de weersituatie op
dat moment met
zich meebrengt. 'Die gebruiker kan
nu zijn eigen afwegingen maken over
wel of niet asfalteren of beton
storten, het afgelasten of laten
doorgaan van een manifestatie of het
al dan niet
meezeulen van
regenkleding tijdens een
wandeltocht.' |
| |
 |
| Tropische cycloon Isabel op 17 december 2003 |
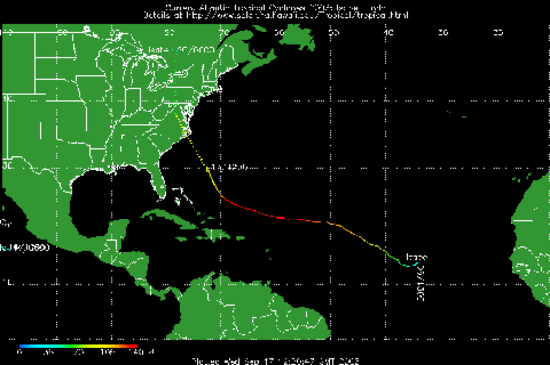 |
| Vergelijking van een deterministische verwachting en een kansverwachting. a). Beginpunt is
de positie van de tropische cycloon Isabel op 17 december 2003.
Satelliet: Seastar. Bron: Institute for Astronomy, University of Hawaiï.
c). |
|
|
|
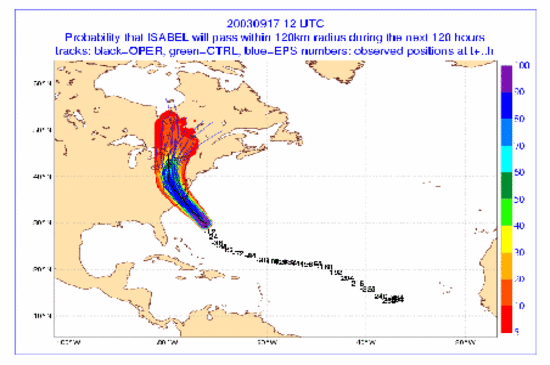
| vijftig mogelijke banen van Isabel
zijn met dunne blauwe lijnen
ingetekend. De kans dat Isabel op
een afstand van 120 kilometer of
minder langstrekt, is aangegeven in
kleuren (zie legenda rechts). Bron:
ECMWF, Reading, UK. |
|
| 15.1 Kansverwachtingen en
gebeurtenissen |
| |
| Met deterministische verwachtingen
is niets mis. Behalve dan dat je er
de mate van onzekerheid die
onlosmakelijk aan weersverwachtingen
kleeft, niet uit kunt destilleren.
Daar komt nog bij
dat die
onzekerheid de ene dag grotere is
dan de andere, zodat de gebruiker
nog minder weet dan hij al dacht.
Een professionele afnemer van
weerinformatie heeft verwachtingen
nodig waarbij de kansen in getallen
worden uitgedrukt, van 0 tot 1, of
in procenten, van nul tot honderd.
Pas dan kan hij een verantwoorde
afweging maken bij het nemen van
besluiten over zijn weergerelateerde
activiteiten. Atmosfeermodellen
kunnen zulke kansgetallen niet
direct leveren. Over sommige
gebeurtenissen doen
atmosfeermodellen zelfs in het
geheel geen uitspraak,
zoals onweer,
windvlagen, vorst aan de grond, mist
en gladheid. Kansverwachtingen zijn
in al deze gevallen wél mogelijk. |
| |
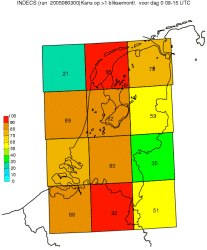
| Een kansverwachting geeft dan de
kans op zo'n gebeurtenis. In het
geval van figuur 2 gaat het om
onweer. Of meer precies, het
optreden van twee of meer
bliksemontladingen zoals waargenomen
door het KNMI-bliksemdetectiesysteem
SAFIR. Er wordt precies bij
aangegeven over welke periode
de verwachting geldt: 3 juni 2005
van 09 tot 15 UTC. Ook de plaats of
het gebied waarop de verwachting
betrekking heeft, ligt vast. In
figuur 2 gaat
het om twaalf verschillende gebieden
zoals met vakken aangegeven; voor
elk vak is een kansverwachting
opgesteld. |
| |
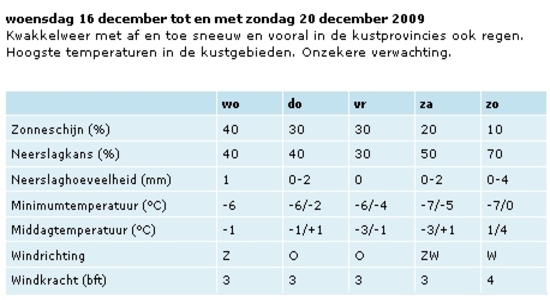
De gebeurtenis waarvoor een
kansverwachting wordt gegeven, is
vaak het overschrijden van een
drempelwaarde: windkracht 8 of meer,
maximumtemperatuur 30 graden of
hoger, neerslaghoeveelheden van ten
minste 5 millimeter, meer dan één
bliksemontlading. Daarom is ook het
woord 'overschrijdingskans' in zwang
(vergelijk figuur 3). Een kans van
dertig procent betekent dat de
gebeurtenis zich in drie van de tien
gevallen
zal voordoen. Een bekend voorbeeld
van een kansverwachting is de
neerslagverwachting voor morgen en
de dagen daarna.
Ze is onder andere
te vinden op NOS-Teletekst,
RTL-tekst (figuur 4) en op
verscheidene websites. Om de
getallen te kunnen interpreteren,
moet je een aantal dingen
weten.
Waar ligt bijvoorbeeld de
grens tussen nat en droog? Doen
sneeuw en hagel ook mee? Slaan de
getallen op het hele etmaal of
gelden ze alleen voor de overdagperiode. Zijn de waarden van
toepassing op het waarneemstation De
Bilt? Gelden ze voor een gebied ter
grootte van Soest
en omstreken en hebben ze buiten dat
gebied geen waarde? Of geven ze een
gemiddelde over Nederland? Als dat
laatste het geval is, hoe is die
middeling dan tot stand gekomen? Het
voorbeeld laat zien hoe belangrijk
het is om nauwkeurig te omschrijven
welke kans gegeven wordt. |
| |
 |
|
Figuur 1A |
|
|
 |
|
Figuur 1B |
|
|
 |
|
Figuur 1C |
|
|
 |
|
Figuur 1D |
|
| 1: Kans in procenten op meer dan één
bliksemontlading in de aangegeven
vakken op 3 juni 2005 tussen 09 en
15 UTC. Bron: KNMI. |
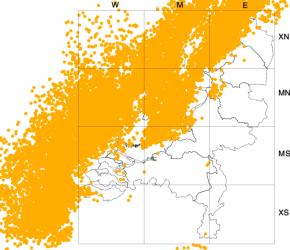
2: Waargenomen bliksemontladingen op
3 juni 2005 tussen 09 en 15 UTC, dus
in hetzelfde tijdvak als waarvoor de
kansverwachting van figuur a
geldig was. Bron: KNMI. |
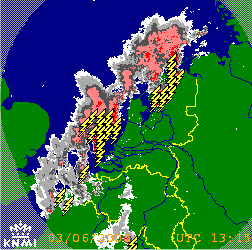
3: Satellietbeeld van 3 juni 2005
13.11 UTC, met onweersbuien boven
Noord-Nederland, langs de Hollandse,
Zeeuwse en Vlaamse kust en boven
Frankrijk. Het waarnemingstijdstip ligt in het tijdvak
waarvoor de kansverwachting van
figuur a geldig was. De
uitwaaierende cirruskappen van de
aambeelden van de onweersbuien zijn vooral boven de
Noordzee goed zichtbaar. Bron: DLR Institut für Physik der Atmosphäre,
Oberpfaffenhofen, Duitsland. |
4: Radarbeeld van 3 juni 2005 13.15
UT, dus van ongeveer dezelfde tijd
als het satellietbeeld van figuur c.
In het radarbeeld zijn locaties met
bliksemontladingen apart aangegeven. Bron: KNMI. |
| |
 |
| Figuur-5 |
|
|
|
| Figuur-6 |
|
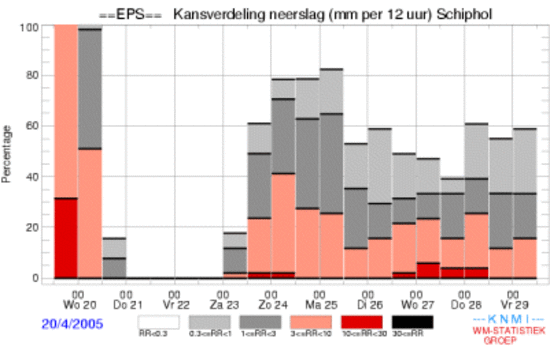
5. Stapeldiagram met
overschrijdingskansen van de
neerslag per twaalf uur op Schiphol.
In de eerste periode van twaalf uur
valt volgens deze
verwachting minstens drie millimeter regen: de grens
van 0,3 millimeter wordt in dat
geval overschreden. Er is een kans
van iets meer dan dertig
procent dat de grens van tien millimeter wordt
overschreden; er valt dan tien tot
dertig millimeter. De figuur bevat
ook vier perioden van twaalf
uur waarin het droog blijft en er dus minder dan 0,3
millimeter regen valt. Bron: KNMI.
|
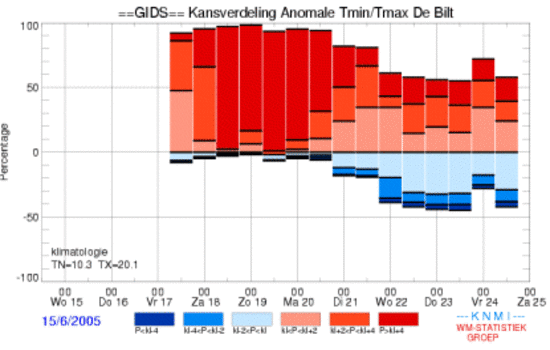
6. Stapeldiagram met
overschrijdingskansen van de
afwijking van de minimum- en
maximumtemperaturen ten opzichte van
het klimatologisch
gemiddelde. Vooral het weekeinde belooft het erg warm te
worden. Bron: KNMI. |
| |
| 15.2 Afleiden van
kansverwachtingen |
| |
| Er zijn verscheidene manieren om
kansverwachtingen te maken. Soms
zijn daarvoor weerkaarten nodig uit
het verleden met het
daarbijbehorende opgetreden weer. De
set weergegevens moet minimaal twee
jaar beslaan, maar langer mag
natuurlijk ook. De weerkaarten geven
een analyse van
een opgetreden weersituatie of een
verwachting voor het tijdstip waarop
de weerwaarnemingen zijn verricht. |
| |
Bij de oudste methode voor het
ontwikkelen van kansverwachtingen
gaat men uit van analyses.
Onderzoekers leiden een statistisch
verband af
tussen die analyses en het
opgetreden weer. Datzelfde verband
gebruiken ze vervolgens om het weer
te bepalen dat bij een door een
atmosfeermodel berekende prognose
hoort. In feite veronderstelt men
daarbij dat die prognose perfect is
en het weer volledig vastlegt.
Om die reden noemt men dit de
Perfect Prog methode (PP). |
| |
Inmiddels weten we dat de prognoses
van atmosfeermodellen niet perfect
zijn en dat ook niet kunnen zijn. De
verschillen tussen een door een
model berekende weerkaart en de
gemeten werkelijkheid zijn doorgaans
groter naarmate het tijdstip
waarvoor de prognose geldt, verder
weg ligt,
al zijn er natuurlijk
uitzonderingen (vergelijk figuur 5).
Daarmee kun je rekening houden
bij
het afleiden van het statistisch
verband tussen weerkaart en
opgetreden weer. Voor elke
verwachtingsperiode worden
modeluitvoer en opgetreden weer
vergeleken om zo het verband te
kunnen afleiden;
vandaar de naam Model Output Statistics (MOS). De formules die
het weer voor 12 uur vooruit geven
uit de bijbehorende weerkaart, zijn
bij deze methode dan ook anders
dan
bij een verwachting voor 6, 18, 24,
48 of 72 uur vooruit. Soms worden
per verwachtingstermijn ook heel
andere voorspelvariabelen gebruikt. |
| |
Een derde manier om kansen te
genereren is gebaseerd op het
Ensemble Predictie Systeem (EPS) van
het Europese Weercentrum.
Het EPS maakt vijftig verschillende
prognoses vanuit onderling net iets
verschillende beginsituaties (zie
Zenit december 2002). Als tien van
de vijftig prognoses
wijzen op
storm, is de kans op storm twintig
procent, enzovoort. Er kunnen alleen
kansen worden gegeven voor
weerelementen die beschikbaar zijn
als modeluitvoer, zoals
windsnelheid, neerslaghoeveelheden
of temperatuur op waarnemingshoogte
(figuur 5); voor PP en
MOS
geldt die beperking niet. Om de EPS-informatie toch te kunnen
gebruiken voor andere te verwachten
variabelen, wordt de uitvoer van het
systeem benut bij het afleiden van
kansen
volgens de MOS-methode. |
 |
| Figuur-8 |
|
|
 |
| Figuur-9 |
|
8. Neerslagverwachtingen op teletekst en op internet voor morgen en de dagen daarna zij doorgaans kansverwachtingen. Ze geven de kans op
neerslag in procenten. |
9. Temperatuurverwachtingen voor De
Bilt volgens het ECMWF-weermodel
(rood in hoge resolutie, blauw in
lage), het Ensemble Predictie
Systeem
(EPS) van het ECMWF (vijftig groene lijnen met een bruin
gemiddelde) en volgens het Model
Output Statistics systeem van het
KNMI
(twee bruine punten per etmaal). De lijnen verbinden de
temperaturen om 00 en 12 UTC; de
bruine punten geven de waarden voor
de
minimumtemperatuur (kort na zonsopkomst) en de
maximumtemperatuur (halverwege de
middag). In dit geval was de
onzekerheid op korte
termijn groter dan iets verder weg, wat vrij ongebruikelijk
is. De temperaturen vertonen dinsdag
en woensdag namelijk een grotere
spreiding
dan de erop volgende donderdag en vrijdag. Bron: KNMI. |
| |
| 15.3 Kloppen
kansverwachtingen? |
| |
Bij kansverwachtingen is het
moeilijker om na te gaan of ze zijn
uitgekomen dan bij deterministische
verwachtingen. Als de kans op regen
dertig procent bedraagt en het
blijft droog,
dan kan dat. Ook als
het gaat regenen hoeft de
verwachting niet fout te zijn; de
kans erop was als volgt uit vergelijking met andere
methoden, zoals het gebruik van de
klimatologie (het gemiddelde weer)
of de persistentie (morgen hetzelfde
weer als vandaag). We willen dat de
kansverwachtingen beter presteren
of, in het jargon, een hogere skill
hebben. De skill van een perfecte,
deterministische verwachting is het
streefdoel, dat overigens nooit zal
worden gehaald.
De kwaliteitsmaten
zijn uit te drukken in getallen, wat
vergelijking en verbetering van
kansverwachtingen mogelijk maakt. |
| |
| 15.4 Wat heb je aan
kansverwachtingen? |
| |
Voor meteorologen die een
weerbericht opstellen, geven de
kansverwachtingen belangrijke
informatie. Ze helpen bij het
onderbouwen van de te verwachten
weersontwikkelingen en het onder
woorden brengen daarvan. Sommige
gebruikers krijgen de getallen van
de kansverwachtingen direct
aangeleverd. Hoeveel profijt dat
oplevert, hangt af van wat ze ermee
willen doen.
Daarbij zijn vooral
belangrijk hoe hoog de schade is die
de gebruiker van een weergebeurtenis
ondervindt en wat het hem kost om
die schade te voorkomen. In het
geval van een fruitteler gaat
het
bijvoorbeeld om nachtvorstschade;
door beregening van zijn boomgaarden
voorkomt hij dat de oogst van een
jaar verloren gaat. Voor een
wegbeheerder zijn het ongelukken
door gladheid,
al of niet gevolgd
door schadeclaims, die hij kan
voorkomen door tijdig wegenzout te
strooien.
Als de schade gering is,
is het niet de moeite waard om
voorzorgsmaatregelen te nemen,
zeker
als daar ook nog een stevig
prijskaartje aan hangt. Als de
schade hoog is,
en het kost weinig
om die te voorkomen, zal men altijd
voorzorgsmaatregelen nemen, ook al
is de kans op schade maar klein. Als
het bedrag van
een eventuele schade,
de kosten van preventie en de
kwaliteit van het systeem van
kansverwachtingen alle nauwkeurig
bekend zijn, kan tot op de euro
nauwkeurig worden aangegeven of een
gebruiker baat heeft bij de
kansverwachtingen en hoeveel geld
hij bespaart. De verhouding tussen
de kosten van preventie en het
schadebedrag bepaalt
de winst.
Als
de kans op de weergebeurtenis
(ditmaal uitgedrukt in een getal
tussen 0 en 1)
groter is
dan die verhouding, moet de
gebruiker actie ondernemen; is die
kans kleiner, dan kan hij beter
niets doen. In de praktijk blijkt
het niet altijd eenvoudig de
bedragen van schade en preventie
vast te stellen. Hoeveel kost een
ten onrechte niet uitgevoerde
lijnvlucht? Hoe bereken je
imagoschade?
Wat is een mensenleven precies
waard? Om deze zaken in kaart te
brengen, is uitvoerig overleg nodig
tussen de aanbieder van de
weerinformatie
en de gebruiker. Vandaar dat er,
naast de aandacht die gaat zitten in
het afleiden van kansverwachtingen,
ook steeds meer werk
wordt gemaakt
van het in kaart brengen van de
manier waarop weerinformatie
bedrijven of overheidsinstellingen
kan helpen schade te voorkomen of
kosten te besparen.
|
| |
|
Bron:
Weerkunde -
Meteorologie voor
iedereen (Kees
Floor) |
|
|
|
|