|
|
|
| Een hypsometer is een meetinstrument om hoogte te meten. De werking berust op het feit dat het kookpunt van een vloeistof verandert naarmate de luchtdruk varieert. Op basis van deze luchtdruk kan dan een hoogte gegeven worden. |
| |
Het instrument bestaat uit een cilindrisch vat waarin een vloeistof - meestal water - wordt verwarmd. In de buitenkant van de buis kan de
waterdamp circuleren, terwijl in het midden een nauwkeurige thermometer staat. Om tot de juiste hoogte te komen zijn tabellen nodig van
kookpunt tegen luchtdruk, en dan van luchtdruk tegen de hoogte. "Hypsos" komt uit het Grieks en betekent stijging, hoogte. |
 |
| Casella Hypsometer (kookpuntthermometer voor hoogte) |
|
|
.png) |
| Hypsometer van André Koehne |
|
|
 |
| (1) Hypsometer Teylers Museum |
|
Het apparaat bestaat uit een cilindrische houder, bijvoorbeeld een glazen buis, waarin een vloeistof (meestal water) aan de kook wordt gebracht.
Een thermokoppel meet continu de temperatuur van de vloeistof (niet de temperatuur van de damp). Om de hoogte van de plaats af te leiden als functie van de gemeten temperatuur, is het nodig om de relatie te kennen tussen kooktemperatuur en druk enerzijds, en de relatie tussen atmosferische druk en hoogte anderzijds. De precisie van de drukmeting is direct gerelateerd aan de precisie van de temperatuurmeting en op lage hoogte is de vereiste precisie in de orde van een honderdste graad. |
| |
Andere vloeistoffen kunnen worden gebruikt, de meest voorkomende zijn ethanol en methanol. Een model van hypsometer werd ontwikkeld door het Amerikaanse leger in de late jaren 1950 met behulp van koolstofdisulfide (CS2) dat niet hoefde te worden verwarmd omdat de verdampingstemperatuur van de vloeistof lager was dan de omgevingstemperatuur, maar de nadelen van het gebruik van dit type vloeistof waren zijn gevaarlijkheid en zijn milieuproblemen. Het voordeel van deze hypsometer was dat hij nauwkeuriger was dan een traditionele Vidie-capsule, vooral bij een druk onder de 50 hPa (19.300 m). |
| Met een eenvoudige hypsometer op schaal kan de hoogte van een gebouw of boom worden gemeten door over een liniaal naar de basis en bovenkant van het te meten object te kijken,
wanneer de afstand van het object tot de waarnemer bekend is. Moderne hypsometers gebruiken een combinatie van laserafstandsmeter en clinometer om afstanden tot de boven- en onderkant van objecten te meten, en de hoek tussen de lijnen van de waarnemer naar elk om de hoogte te berekenen. |
 |
| Nikon Foresters laser-afstandsmeter-hypsometer |
|
|
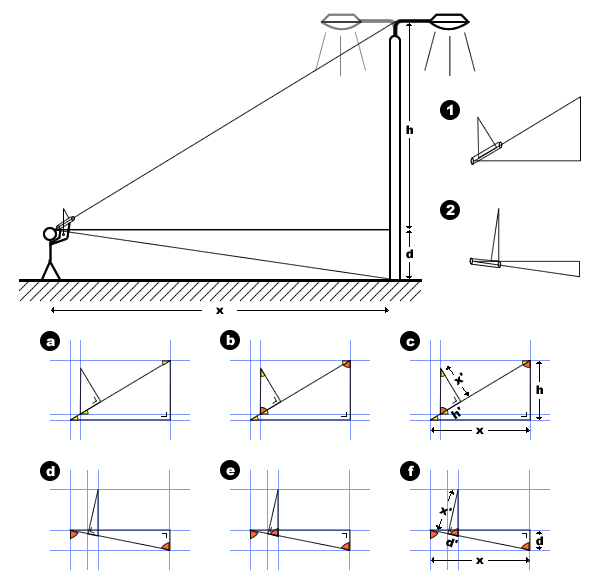 |
| Hypsometer schaal |
|
| Een voorbeeld van een
dergelijke hypsometer met
schaal wordt hier
geïllustreerd en kan worden
gezien als een kijkbuis, een
vaste horizontale schaal en
een verstelbare verticale
schaal met daaraan bevestigd
schietlood. Het
werkingsprincipe van een
dergelijke schaalhypsometer
is gebaseerd op het idee van
vergelijkbare driehoeken in
de geometrie. Eerst wordt de
verstelbare verticale schaal
op een geschikte hoogte
ingesteld. Vervolgens wordt,
zoals in stap 1 in de
afbeelding, een waarneming
gemaakt op de bovenkant van
het object waarvan de hoogte
moet
worden bepaald, en de
aflezing op de horizontale
schaal, h ', geregistreerd.
Berekening op basis van deze
waarde geeft uiteindelijk de
hoogte h, vanaf de ooglijn
van de waarnemer tot de
bovenkant van het object
waarvan de hoogte moet
worden bepaald. |
| |
| Op dezelfde manier als in
stap 2 van de illustratie
wordt een waarneming gemaakt
op de basis van het object
waarvan de hoogte moet
worden bepaald, en wordt de
aflezing op de horizontale
schaal, d ', geregistreerd.
Berekening op basis van deze
waarde geeft uiteindelijk de
afstand van de basis van het
object tot de ooglijn van de
waarnemer. Ten slotte moet
de afstand x van de
waarnemer tot het object
worden gemeten. |
| |
| Kijkend naar de geometrie
van stap 1 resulteert in
schets a: twee rechthoekige
driehoeken, hier weergegeven
met dezelfde kleine hoeken
in geel. Vervolgens zien we
in schets b dat de twee
driehoeken identieke hoeken
hebben - elk heeft een
rechte hoek, dezelfde kleine
hoek weergegeven in geel en
dezelfde grotere hoek
weergegeven in oranje.
Daarom zien we in schets c
dat
door gebruik te maken
van het principe van
gelijkaardige driehoeken,
aangezien elke driehoek
identieke hoeken heeft, de
zijden in verhouding zullen
zijn: x de afstand tot het
object in
verhouding tot x
', de hoogte ingesteld op de
verticale schaal van de
hypsometer, en h de hoogte
van het object boven de
ooglijn van de waarnemer in
verhouding tot h ', de
aflezing van de horizontale
schaal van de hypsometer. |
| |
Gegeven dat Tan (kleine gele
hoek) = tegenoverliggende
zijde / aangrenzende zijde,
dus Tan (kleine gele hoek) =
h / x = h '/ x'. Daarom h = h'x / x '. |
| |
Evenzo resulteert de
geometrie van stap 2 in
schets d: twee rechthoekige
driehoeken. Vervolgens zien
we in schets e dat de twee
driehoeken weer identieke
hoeken hebben - elk heeft
een rechte hoek, dezelfde
kleine hoek weergegeven in
geel en dezelfde grotere
hoek weergegeven in oranje.
Daarom zien we in schets f
dat door gebruik te maken
van het principe van
gelijkaardige driehoeken,
aangezien elke driehoek
identieke hoeken heeft, de
zijden in verhouding zullen
zijn: x de afstand tot het
object in verhouding tot x
', de hoogte ingesteld op de
verticale schaal van
de
hypsometer,
en d de diepte
van het object onder de
ooglijn van de waarnemer in
verhouding tot d ', de
aflezing van de horizontale
schaal van de hypsometer. |
| |
| Gegeven dat Tan (kleine
hoek) = tegenoverliggende
zijde / aangrenzende zijde,
dus Tan (kleine hoek) = d /
x = d '/ x'. Daarom d = d'x
/ x '. |
| |
| De totale hoogte van het
object is dus x (d '+ h') /
x '
|
| Luchtdruk (hPa) |
Temperatuur waterdamp (C). |
| 960 |
98,49 |
| 980 |
99,07 |
| 1000 |
99,63 |
| 1020 |
100,18 |
| 1040 |
100,73 |
|
|
| De kooktemperatuur van een vloeistof is afhankelijk van de luchtdruk. Figuurlijk gesproken bemoeilijkt een hogere luchtdruk de overgang van een deeltje van de vloeibare naar de gasfase. H. bij hogere druk kookt de vloeistof bij hogere temperaturen, bij lagere druk dienovereenkomstig bij lagere temperaturen. |
| |
Op de hypsobarometer wordt de temperatuur bij het kookpunt afgelezen en hieruit wordt de luchtdruk berekend. Als de bodemdruk bekend is, kan uit de kooktemperatuur het zeeniveau worden bepaald. Bij normale druk kookt water op zeeniveau bij 100 ° C.
|
| |
| De evenwichtstoestand tussen vloeibaar en gasvormig water wordt met een goede benadering beschreven door de Clausius-Clapeyron-vergelijking. Dit meetprincipe wordt beperkt door de lichte daling van de temperatuur van het
kookpunt per hPa van slechts 0,049 K. Dat betekent dat de temperatuurmeetschaal een zeer hoge resolutie moet
hebben (0,01 ° C tot 0,02 ° C). Een bereik van 95–105 ° C is echter voldoende. |
| |
| Hypsothermometer |
| Hypsothermometer |
| Temperatuur (°C). |
Luchtdruk |
Hoogte |
| 82 |
384,4 |
5431 m |
| 84 |
416,3 |
4797 m |
| 86 |
450,3 |
4170 m |
| 88 |
486,6 |
3551 m |
| 90 |
525,4 |
2940 m |
| 92 |
566,7 |
2337 m |
| 94 |
610,7 |
1742 m |
| 96 |
657,4 |
1133 m |
| 98 |
707,2 |
573 m |
| 100 |
760,0 |
0 m |
|
|
| Een hypsothermometer (Grieks; ook thermohypsometer, barothermometer, thermobarometer) is een apparaat voor barometrische hoogtemeting ontwikkeld door Daniel Gabriel Fahrenheit in 1724. |
| |
| Het belangrijkste onderdeel van het apparaat is een thermometer, die alleen temperaturen tussen 80 en 101 ° C aangeeft, maar is opgedeeld in 1 / 1.000 graden. Zo kunnen duizendsten van een graad nog met enige zekerheid worden afgelezen. |
| |
Als men met dit instrument waar dan ook de temperatuur van waterdamp bepaalt,
die wordt gevormd door kokend
water in een open vat, dan verkrijgt men de op het moment van waarneming heersende luchtdruk, aangezien de kooktemperatuur afhangt van de luchtdruk. Hiervoor voegt u een geschikt geconstrueerd kookvat toe aan de kookthermometer, beide vormen samen de hypsothermometer. |
| |
| De tabel kan de relatie tussen de kooktemperatuur en de barometerstand illustreren: |
| Bronnen: Wikipedia-fr, Wikipedia-en, Wikipedia-de, (1) Teylers |
|
|
|
|
|
|
|