|
|
|
| Het corioliseffect, genoemd naar de Franse ingenieur Gustave-Gaspard Coriolis, die het in 1835 voor het eerst beschreef, verklaart de afbuiging van de baan van een voorwerp dat beweegt in een roterend systeem. Het is vooral duidelijk bij de beweging van wolkenmassa's rond een lagedrukgebied die niet recht naar het centrum stromen maar eromheen cirkelen. Op het noordelijk halfrond gebeurt dit tegen de wijzers van de klok in, op het zuidelijk halfrond met de wijzers mee. Dit staat bekend als de wet van Buys Ballot. Een hogedrukgebied kent hetzelfde effect met een draaiing in tegengestelde zin. |
| |
 |
| Afbeelding-1 |
|
|
 |
| Afbeelding-2 |
|
|
 |
| Afbeelding-3 |
|
| |
| 1: Het corioliseffect zichtbaar bij de orkaan Elena |
2: De draairichting van dit lagedrukgebied, dat voor de kust van IJsland draait, is tegen de klok in en is het gevolg van de gecombineerde effecten
van de Corioliskracht en de drukgradiënt. |
| 3: Een wiskundige simulatie met het Coriolis-effect van de beweging van een orkaan. Bekijk in een traagheidsreferentiesysteem. |
| |
| |
In de 15e eeuw was bekend dat de wind op het noordelijk halfrond een lus vormde die naar rechts draaide (met de klok mee). Portugese zeevaarders die de kust van Afrika volgden op zoek naar de zeeroute naar India, stuitten op tegenwind buiten de evenaar. Bartolomeu Dias had het idee dat deze winden ook een lus vormen die naar links draait (tegen de klok in). Hij gebruikte deze intuïtie om sneller richting het zuiden van Afrika
te navigeren en ontdekte zo Kaap de Goede Hoop. |
| |
| Jezuïet-astronoom Giovanni Battista Riccioli en zijn assistent Francesco Maria Grimaldi beschreven het effect in 1651 in Almagestum Novum en zeiden dat het effect van de rotatie van de aarde het traject van een kanonskogel, die naar het noorden werd afgevuurd, naar het oosten moest afbuigen. In zijn Cursus seu Mundus Mathematicus, gepubliceerd in 1674, gebruikte Claude François Milliet Dechales, een jezuïet en anti-Copernicaan als Riccioli, het feit dat deze afwijkingen niet werden waargenomen als argument dat de aarde niet draaide. |
| |
Aan het einde van de 18e eeuw en het begin van de 19e eeuw onderging de mechanica grote theoretische ontwikkelingen. Als ingenieur is Gaspard-Gustave Coriolis geïnteresseerd in het toepasbaar maken van de theoretische mechanica bij het begrijpen en ontwikkelen van industriële machines.
In zijn artikel Over de vergelijkingen van de relatieve beweging van systemen van lichamen4 (1835) beschrijft Coriolis op wiskundige wijze de kracht die zijn naam zal dragen. In dit artikel verschijnt de Corioliskracht als een extra component van de middelpuntvliedende kracht, eveneens traagheidskracht, die wordt gevoeld door een bewegend lichaam ten opzichte van een roterend referentiekader, zoals bijvoorbeeld zou kunnen optreden in de tandwielen van een machine. |
| |
| Het Coriolis-argument is gebaseerd op een analyse van arbeid en potentiële en kinetische energie in roterende systemen. Tegenwoordig maakt de meest gebruikte demonstratie om de Corioliskracht te onderwijzen gebruik van kinematische hulpmiddelen. Pas aan het einde van de 19e eeuw verscheen deze kracht in de meteorologische en oceanografische literatuur. De term ‘Corioliskracht’ verscheen aan het begin van de 20e eeuw. |
| |
| |
| In de Newtoniaanse mechanica wordt de Coriolis-kracht beschreven als een fictieve of traagheidskracht vanwege het feit dat deze alleen bestaat omdat de waarnemer zich in een roterend referentiekader bevindt terwijl er geen kracht wordt uitgeoefend op een waarnemer in een Galilees referentiekader. of inertiaal referentiekader). |
| |
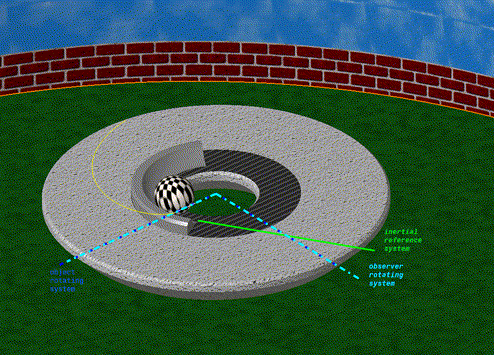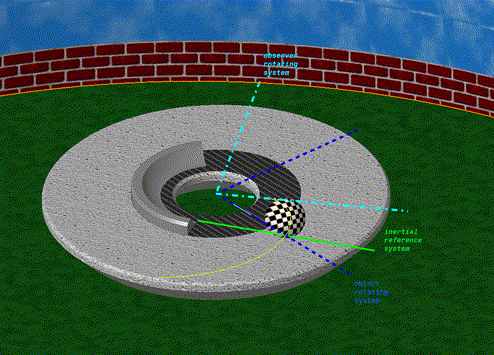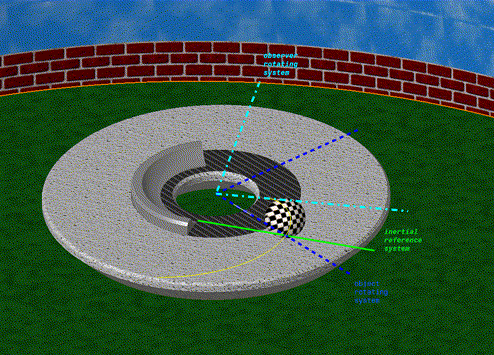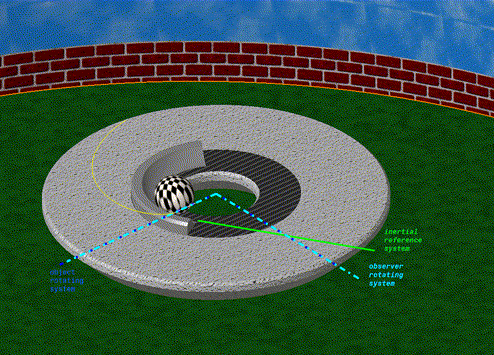
| De animatie rechts toont het verschil tussen bovenaan het gezichtspunt van een stationaire waarnemer in een traagheidsframe buiten het systeem en onderaan dat van een waarnemer die beweegt met een roterende schijf in dezelfde opslagplaats. In beide gevallen is er geen wrijving tussen de zwarte bal en de schijf en dus geen echte kracht. Voor de eerste waarnemer beweegt de bal alleen met een constante snelheid van het midden van de schijf naar de rand. Voor hem komt er geen kracht bij kijken en beweegt de bal in een rechte lijn. |
| |
Voor de tweede, de rode stip, staat de schijf stil en beweegt de bal langs een cirkelboog naar links, waarbij hij voortdurend van richting verandert.
Er is dus een kracht nodig om deze beweging te verklaren. |
| |
| Deze pseudo-kracht is de Coriolis-kracht.Het staat loodrecht op de rotatieas van het referentieframe en op de vector van de snelheid van het bewegende lichaam. Als het lichaam zich van de rotatie-as af beweegt, wordt het in de tegenovergestelde rotatierichting uitgeoefend. Als het lichaam de rotatieas nadert, wordt het in dezelfde richting uitgeoefend als de rotatie. |
| |
4: Baan van een zwarte bal met constante snelheid, van bovenaf
gezien voor een roterende schijf met een rode stip op de rand.
Voor een stilstaande waarnemer van buitenaf is het een
rechte lijn (omhoog). Voor een waarnemer die zich op het
rode punt (onder) bevindt, volgt dit de omgekeerde curve van
de rotatie. Situatie vergelijkbaar met de vorige, maar gezien
met een horizontale beweging zonder wrijving. |
| |
5: Situatie vergelijkbaar met de vorige, maar gezien met
wrijvingsloze horizontale beweging. |
|
|
 |
| Afbeelding-4 |
|
|
 |
| Afbeelding-5 |
|
| |
| Corioliskracht en axifugale kracht |
In het eerder geziene beeld van de schijf en de bal glijdt deze zonder wrijving en is alleen de Coriolis-kracht aanwezig in het roterende frame.
In het geval van de beweging van een lichaam op het aardoppervlak, heeft dit laatste zijn eigen beweging op het aardoppervlak. Het beweegt zich ook door de ruimte, met de rotatie van de planeet, en wordt aangetrokken door de zwaartekracht. Het wordt daarom ook onderworpen aan een andere fictieve kracht, de drijvende traagheidskracht. |
| |
Drijvende kracht omvat verschillende termen, waaronder middelpuntvliedende kracht. Zoals eerder gezien, hangt de Coriolis-kracht af van de
snelheid van het bewegende lichaam. De middelpuntvliedende kracht, in werkelijkheid de axifuge-kracht, wordt gedefinieerd en hangt af van de
positie (R) van het lichaam ten opzichte van de momentane rotatie-as. Deze twee krachten kunnen variëren als ze variëren, maar voor een
gegeven kunnen we zeggen dat de middelpuntvliedende kracht de middelpuntvliedende kracht is. statische component van de traagheidskracht die zich manifesteert in het roterende referentiekader, terwijl de Corioliskracht de kinematische component is (zie traagheidskrachten). We moeten ook rekening houden met de orthocentrifugale traagheidskracht, anders zou de analyse verkeerd zijn. |
| |
| Meteorologie en oceanografie |
| |
| Misschien wel de belangrijkste impact van het Coriolis-effect ligt in de grootschalige dynamiek van de oceanen en de atmosfeer. In de meteorologie en oceanografie is het handig om een roterend referentiekader te veronderstellen waarin de aarde stilstaat. Ter aanpassing aan dit voorlopige uitgangspunt worden de centrifugaal- en Corioliskrachten geïntroduceerd. Hun relatieve belang wordt bepaald door de toepasselijke Rossby-getallen. Tornado's hebben hoge Rossby-getallen, dus hoewel de met tornado's geassocieerde centrifugaalkrachten behoorlijk substantieel zijn, zijn de Coriolis-krachten die met tornado's worden geassocieerd voor praktische doeleinden verwaarloosbaar. |
| |
| Omdat oppervlakte-oceaanstromingen worden aangedreven door de beweging van de wind over het wateroppervlak, beïnvloedt de Coriolis-kracht ook de beweging van oceaanstromingen en cyclonen. Veel van de grootste stromingen in de oceaan circuleren rond warme hogedrukgebieden die gyres worden genoemd. Hoewel de circulatie niet zo belangrijk is als die in de lucht, is het de afbuiging veroorzaakt door het Coriolis-effect die het spiraalvormige patroon in deze gyres creëert. Het spiraalvormige windpatroon helpt de orkaan te vormen. Hoe sterker de kracht van het Coriolis-effect, hoe sneller de wind draait en extra energie oppikt, waardoor de kracht van de orkaan toeneemt |
| |
| Lucht in hogedruksystemen roteert in een zodanige richting dat de Coriolis-kracht radiaal naar binnen is gericht en bijna in evenwicht wordt gehouden door de naar buiten gerichte radiale drukgradiënt. Als gevolg hiervan beweegt de lucht zich met de klok mee rond de hogedruk op het noordelijk halfrond en tegen de klok in op het zuidelijk halfrond. Lucht rond lage druk roteert in de tegenovergestelde richting, zodat de Coriolis-kracht radiaal naar buiten is gericht en bijna een naar binnen gerichte radiale drukgradiënt in evenwicht houdt. |
 |
| Afbeelding-5 |
|
|
 |
| Afbeelding-6 |
|
|
 |
| Afbeelding-6 |
|
| |
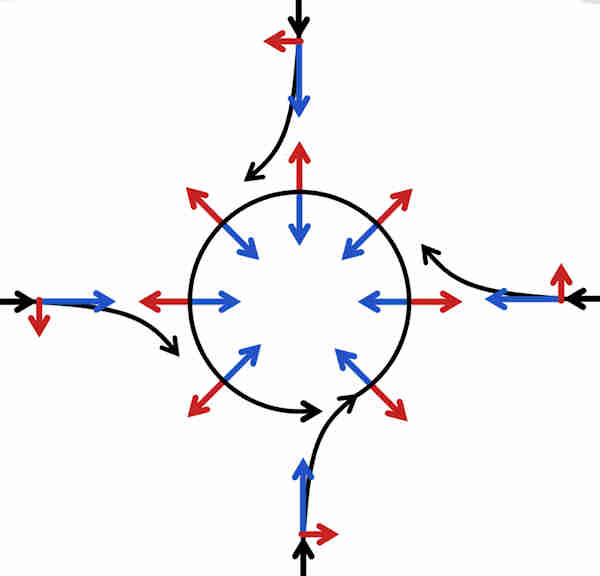
5: Schematische weergave van stroming rond een lagedrukgebied op het noordelijk halfrond. Het Rossbygetal is laag, dus de middelpuntvliedende
kracht is vrijwel te verwaarlozen. De drukgradiëntkracht wordt weergegeven door blauwe pijlen, de Coriolis-versnelling (altijd loodrecht op de
snelheid) door rode pijlen |
6: Schematische weergave van traagheidscirkels van luchtmassa's bij afwezigheid van andere krachten, berekend voor een windsnelheid van
ngeveer 50 tot 70 m/s. |
| 7: Wolkenformaties in een beroemd beeld van de aarde van Apollo 17 maken soortgelijke circulatie direct zichtbaar |
| |
| Stroming rond een lagedrukgebied |
| Als zich in de atmosfeer een lagedrukgebied vormt, heeft de lucht de neiging ernaartoe te stromen, maar wordt door de Corioliskracht loodrecht op de snelheid afgebogen. Een systeem van evenwicht kan zich dan vestigen door een cirkelvormige beweging of een cyclonische stroom te creëren. Omdat het Rossbygetal laag is, ligt het krachtevenwicht grotendeels tussen de drukgradiëntkracht die naar het lagedrukgebied werkt en de Corioliskracht die weg werkt van het centrum van de lage druk. |
| |
| In plaats van langs de gradiënt te stromen, hebben grootschalige bewegingen in de atmosfeer en de oceaan de neiging loodrecht op de drukgradiënt plaats te vinden. Dit staat bekend als geostrofische stroming. Op een niet-roterende planeet zou vloeistof langs de meest recht mogelijke lijn stromen, waardoor drukgradiënten snel worden geëlimineerd. Het geostrofische evenwicht is dus heel anders dan het geval van traagheidsbewegingen (zie hieronder), wat verklaart waarom cyclonen op de middelste breedtegraad een orde van grootte groter zijn dan de traagheidscirkelstroom zou zijn. |
| |
Dit afbuigingspatroon en de bewegingsrichting worden de wet van Buys-Ballot genoemd. In de atmosfeer wordt het stromingspatroon een cycloon genoemd. Op het noordelijk halfrond is de bewegingsrichting rond een lagedrukgebied tegen de klok in. Op het zuidelijk halfrond is de bewegingsrichting met de klok mee omdat de rotatiedynamiek daar een spiegelbeeld is. Op grote hoogte roteert de naar buiten verspreidende lucht
in de tegenovergestelde richting. Cyclonen vormen zich zelden langs de evenaar vanwege het zwakke Coriolis-effect dat in deze regio aanwezig is. |
| |
| Traagheidscirkels |
| Een lucht- of watermassa die met snelheid beweegt en alleen onderhevig is aan de Coriolis-kracht, beweegt zich in een cirkelvormig traject dat een traagheidscirkel wordt genoemd. |
| |
| De Coriolis-parameter heeft doorgaans een waarde op de middelste breedtegraad van ongeveer 10−4 s, vandaar dat voor een typische atmosferische snelheid van 10 m / s met een straal van 100 km is met een periode van ongeveer 17 uur. Voor een zeestroming met een typische snelheid van 10 cm/s is de straal van een traagheidscirkel 1 km.. Deze traagheidscirkels zijn met de klok mee op het noordelijk halfrond (waar trajecten naar rechts zijn gebogen) en tegen de klok in op het zuidelijk halfrond. |
| |
| Als het roterende systeem een parabolische draaitafel is, dan is het constant en zijn de trajecten exacte cirkels. Op een roterende planeet varieert de breedtegraad en vormen de paden van deeltjes geen exacte cirkels. Omdat de parameter varieert als de sinus van de breedtegraad, is de straal van de oscillaties die bij een bepaalde snelheid horen het kleinst bij de polen (breedtegraad van ± 90 °), en neemt deze toe richting de evenaar. |
| |
| Andere aardse effecten |
| Het Coriolis-effect heeft een sterke invloed op de grootschalige oceanische en atmosferische circulatie, wat leidt tot de vorming van robuuste kenmerken zoals straalstromen en westelijke grensstromen. Dergelijke kenmerken zijn in geostrofisch evenwicht, wat betekent dat de Coriolis- en drukgradiëntkrachten elkaar in evenwicht houden. Coriolisversnelling is ook verantwoordelijk voor de voortplanting van vele soorten golven in de oceaan en de atmosfeer, waaronder Rossby-golven en Kelvin-golven. Het speelt ook een belangrijke rol bij de zogenaamde Ekman-dynamiek in de oceaan, en bij het tot stand brengen van het grootschalige oceaanstromingspatroon dat de Sverdrup-balans wordt genoemd. |
| |
| Eötvös-effect |
| De praktische impact van het "Coriolis-effect" wordt grotendeels veroorzaakt door de horizontale versnellingscomponent die wordt geproduceerd door horizontale beweging |
| |
Er zijn nog andere componenten van het Coriolis-effect. Westwaarts reizende objecten worden naar beneden afgebogen, terwijl oostwaarts
reizende objecten naar boven worden afgebogen. Dit staat bekend als het Eötvös-effect. Dit aspect van het Coriolis-effect is het grootst nabij de evenaar. De kracht geproduceerd door het Eötvös-effect is vergelijkbaar met de horizontale component, maar de veel grotere verticale krachten als gevolg van zwaartekracht en druk suggereren dat deze onbelangrijk is in het hydrostatische evenwicht. In de atmosfeer worden winden echter geassocieerd met kleine drukafwijkingen ten opzichte van het hydrostatische evenwicht. In de tropische atmosfeer is de orde van grootte van de drukafwijkingen zo klein dat de bijdrage van het Eötvös-effect aan de drukafwijkingen aanzienlijk is. |
| |
Bovendien worden objecten die naar boven (dat wil zeggen naar buiten) of naar beneden (dat wil zeggen naar binnen) reizen, respectievelijk naar
het westen of oosten afgebogen. Dit effect is ook het grootst nabij de evenaar. Omdat verticale beweging doorgaans een beperkte omvang en duur heeft, is de omvang van het effect kleiner en zijn er nauwkeurige instrumenten nodig om deze te detecteren. Geïdealiseerde numerieke modelleringsstudies suggereren bijvoorbeeld dat dit effect het tropische grootschalige windveld direct met ongeveer 10% kan beïnvloeden, gegeven langdurige 2 weken of meer verwarming of koeling in de atmosfeer. Bovendien wordt het effect aanzienlijk in het geval van grote veranderingen in het momentum, zoals wanneer een ruimtevaartuig in een baan om de aarde wordt gelanceerd. Het snelste en meest brandstofefficiënte pad naar
een baan om de aarde is een lancering vanaf de evenaar met een bocht naar een directe oostelijke richting. |
| |
| Driedimensionale Coriolis |
| Omdat de aarde niet plat is en de atmosfeer een bepaalde dikte heeft, hebben bewegingen naast een horizontale component doorgaans ook een verticale component. De Corioliskracht wordt daarom niet alleen parallel aan het oppervlak van de planeet uitgeoefend, maar ook verticaal. Een luchtpakketje aan het oppervlak zou bijvoorbeeld in de draairichting van de aarde naar een ster aan het firmament kunnen bewegen. Terwijl deze laatste roteert, verandert het oppervlak van richting ten opzichte van deze oriëntatie en lijkt de plot naar boven te bewegen, vandaar een pseudokracht die hem in deze richting trekt. |
| |
| Dit effect is erg zwak omdat de Corioliskracht weinig tijd heeft om zich uit te oefenen voordat het luchtdeeltje de boven- of ondergrens van de atmosfeer bereikt, maar bepaalde objecten beïnvloedt, zoals ballistische schoten. De effecten verschillen afhankelijk van de richting: |
| |
| - een dalend luchtpakket zal enigszins naar het oosten worden afgebogen. |
| - een andere stijging zal naar het westen worden afgebogen. |
| - een oostwaartse beweging zal licht stijgen. |
| - een westwaartse beweging zal iets dalen. |
| |
| De rotatie van een tornado is meestal tegen de klok in op het noordelijk halfrond, en omgekeerd op het zuidelijk halfrond, maar dit is niet direct te wijten aan de Corioliskracht. 1 tot 2% van de tornado's doet echter het tegenovergestelde, de zogenaamde anticyclonische tornado's. |
| |
| De rotatie wordt eerst geïnitieerd door windschering in de luchtlaag nabij de grond, wat resulteert in een horizontale luchtwerveling. Wanneer de sterke opwaartse beweging van een storm deze rotatie vertikaliseert en geconcentreerd raakt, is de richting al bepaald19. We bevinden ons hier opnieuw in een domein waar de beweging van de lucht veel te snel is om het Coriolis-effect de tijd te geven om invloed uit te oefenen op de vortex. Het enige dat de Corioliskracht heeft beïnvloed is de configuratie op synoptische schaal van de winden boven de atmosferische grenslaag, maar de effecten van reliëf spelen lager in het spel (zie de Ekman-spiraal), wat de windschering aanzienlijk kan veranderen. |
| |
 |
| Windschering zorgt voor horizontale rotatie |
|
|
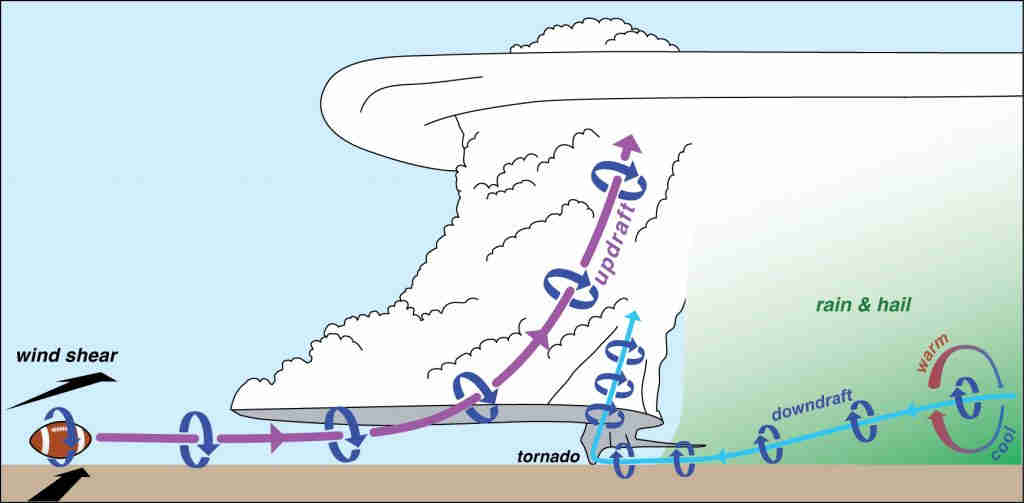 |
| Kantelen van de vortex door de stijgende stroom |
|
| |
| In het geval van een stofwerveling wordt de rotatie geïnitieerd door een verschil in horizontale wind. We hebben dan een verticale as van vortex gecreëerd waar de middelpuntvliedende kracht wordt gecompenseerd door die van de druk. De snelheid van de deeltjes is te hoog en heeft een te kleine straal om de Corioliskracht de tijd te geven om in te werken. Waarnemingen hebben aangetoond dat de rotatie in deze wervels statistisch gelijk verdeeld is tussen rechtsom en linksom, ongeacht het halfrond. |
| |
|
|
|
|
|
|