|
|
|
| Dit fenomeen heeft niet alleen invloed op lichtstralen, maar in het algemeen op alle elektromagnetische golven. Het effect is ook een functie van de golflengte (dispersiefenomeen). Blauw licht wordt dus meer beïnvloed dan rood licht door het fenomeen. Dit is de reden waarom astronomische objecten, vanwege hun spectrum, hun afbeeldingen met hoge resolutie kunnen zien uitgespreid. De groene straal kan gedeeltelijk ook worden geïnterpreteerd door atmosferische breking en dispersie. Het zien van de zon aan de horizon in een langwerpige, enigszins afgeplatte vorm is een ander effect van atmosferische breking, ook waarneembaar voor de Maan. |
| |
Atmosferische breking is veel groter voor objecten nabij de horizon dan voor objecten dichter bij het zenit. Dus om de effecten te beperken,
plannen astronomen hun objectobservaties zoveel mogelijk op het hoogste punt van hun baan in de lucht. Evenzo richten zeelieden zich voor begeleiding niet op sterren dicht bij de horizon, maar alleen op sterren die ten minste 20 ° erboven staan. Als waarnemingen dicht bij de horizon
niet kunnen worden vermeden, is het op bepaalde optische instrumenten mogelijk om de verschuivingen als gevolg van atmosferische breking en
de effecten van dispersie te compenseren. |
| |
Atmosferische breking hangt echter ook af van atmosferische druk en temperatuur. De systemen die het mogelijk maken om alle effecten correct
te compenseren, zijn technologisch gecompliceerd en vaak onbetaalbaar. Het probleem is nog gecompliceerder wanneer de atmosferische breking niet-homogeen is, in het bijzonder wanneer er turbulentie in de lucht is. Deze turbulentie ligt aan de oorsprong van het fenomeen sterscintillatie. |
 |
| Foto-1 |
|
|
 |
| Foto-2 |
|
| |
1: Foto van de maan gedeeltelijk verduisterd door de atmosfeer van de aarde, genomen vanaf de Space Shuttle Discovery. De schijnbare vorm
van de maan in het onderste deel is niet langer cirkelvormig vanwege atmosferische breking. |
2: Terrestrische breking: zonsondergang boven de Egeïsche Zee, ongeveer 10 keer vergroot. Zonder breking zou de zon 120% van zijn diameter
lager zijn. De linkerrand van de zon vertoont een kleine brekingsafwijking. |
| |
| Numerieke waarden |
| |
| - De breking neemt toe als de druk toeneemt en neemt af als de druk afneemt (1% per 10 millibar) |
- De breking neemt toe wanneer de temperatuur daalt en het neemt af wanneer de temperatuur stijgt - warme lucht is minder dicht,
het effect is zwakker - (1% per 2,8 ° C). |
| |
Als de ster in het zenit staat, is er geen correctie nodig, aangezien de lichtstraal bij normale inval niet wordt afgebogen. Op 45 ° hoogte is de
correctie bijna een boogminuut waard (1/60 van een graad). Aan de horizon (0° hoog) is het 34', oftewel ongeveer een halve graad. De waarde
die wordt gebruikt in de directory van het Bureau des Longitudes is echter 36'36 ". De schijnbare diameter van de zon is ook bijna een halve graad (32 '), wat verklaart waarom het soms zegt dat: "wanneer de zon de horizon raakt, is deze in werkelijkheid al onder". |
| |
|
|
|
Diagram dat de verschuiving toont tussen de werkelijke positie en de schijnbare positie van de zon aan de horizon. S (in geel) is de actuele
positie. S '(in het rood) is de schijnbare positie
gezien door de waarnemer O op de grond. De blauwe lijn stelt de horizon voor. |
| |
Voor de berekening van de zonsopgang- en zonsondergangtijden wordt ook rekening gehouden met atmosferische breking. De berekende tijd
komt niet overeen met het moment waarop de zon een hoogte van 0 ° bereikt, maar wanneer deze hoogte -50 ' bereikt: zelf de som van twee gegevens: -16' om rekening te houden met de hoekstraal van de zon, deze waarde overeenkomend met de schijnbare halve diameter van de ster uitgedrukt in minuten (de astronomische tabellen geven over het algemeen zijn heliocentrische positie aan) en -34 'voor de atmosferische breking aan de horizon. In het geval van de maan moet rekening worden gehouden met het fenomeen parallax, de hoekdiameter en de maanfase (zelfs als dit laatste punt zelden in aanmerking wordt genomen). |
| |
| |
De Arabische Alhazen bestudeerde de atmosferische breking rond het jaar 1000 door zich te concentreren op de schemering en te ontdekken
dat het fenomeen ophoudt (of begint) wanneer de zon door een positie 19° boven de horizon gaat. De Chinese astronoom Shen Kuo stelde
rond het jaar 1050 ook een interpretatie voor van de regenboog met behulp van atmosferische breking. |
| |
Vóór 1602 was Tycho Brahe in het Westen de eerste die door observatie de waarde van de breking vaststelde met de azimutmethode
(Astronomiae instauratae progymnasmata, 1602):
hij meet de azimut van de zon of van een ster om daaruit zijn ware zenitafstand,
dan meet het de schijnbare zenitafstand van dezelfde ster. Het verschil in zenitafstanden geeft de corresponderende brekingshoek. |
| |
| Kepler in de Paralipomena to Vitellion (1604) publiceert de eerste tafel in het Westen, na het werk van Alhazen in 1603 te hebben gelezen en de observaties van zijn leermeester Tycho Brahé
te raadplegen. In 1637 werd door Descartes de wet van breking van licht ontwikkeld tijdens de passage door een medium met een andere dichtheid dan het oorspronkelijke medium. |
| |
 |
| Altazimuth kwadrant door Tycho Brahe (1602). |
|
|
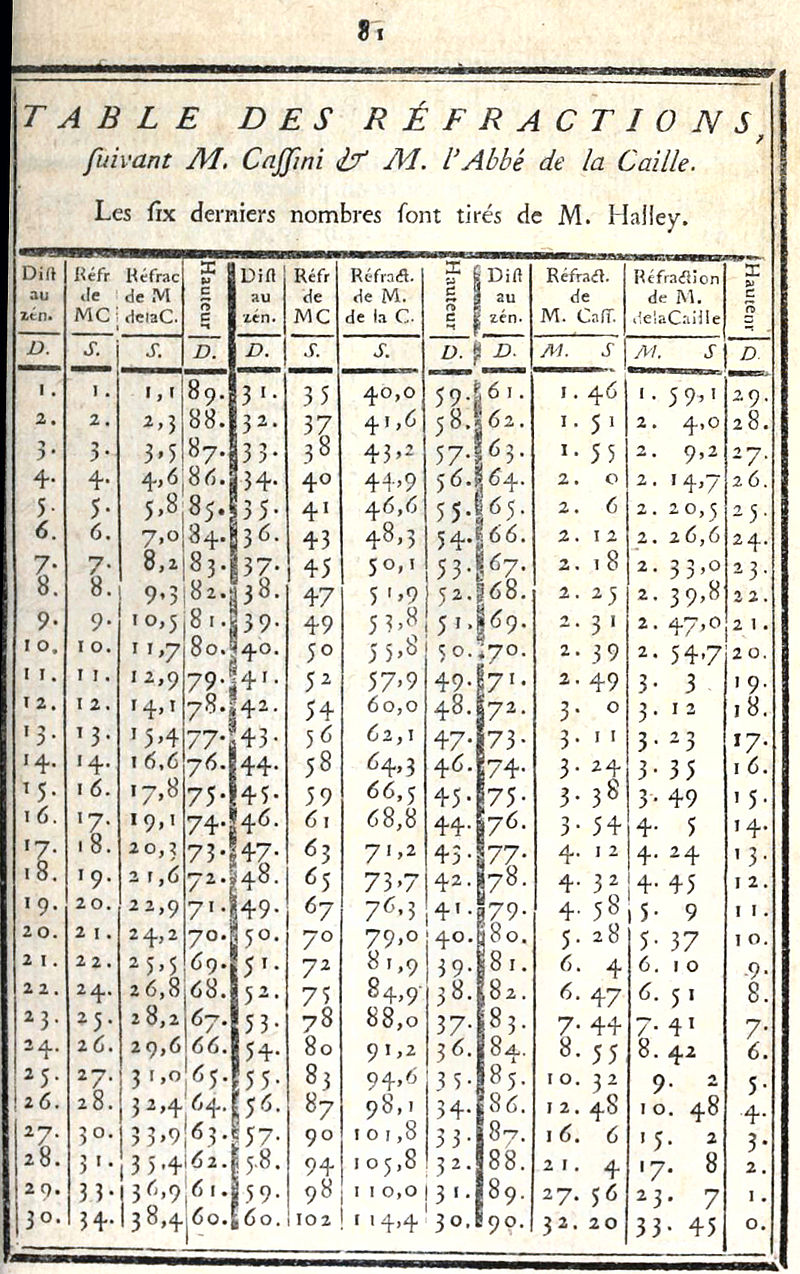 |
| Brekingstabel naar Cassini (1684) en La Caille (1750), ed. 1763. |
|
In 1662 zal Jean-Dominique Cassini het fenomeen modelleren op basis van twee waarnemingen: een aan de horizon met een breking
R = 32 '20" en de andere op 80 ° zenitafstand waar de breking r = 5 '28"; hij leidt de dikte van de atmosfeer af, zogenaamd homogeen,
in de orde van 4 km, die hij voor zijn model zal gebruiken. Dit laatste stelt hem in staat om de waarde van r voor elke graad van z te verkrijgen
en daaruit een eerste tabel te trekken. Een tweede, nauwkeuriger tabel zal in 1684 worden gepubliceerd; het zal tot 17659 worden opgenomen
in de Connaissance des temps. |
| |
| In 1814 vereenvoudigde Delambre de Cassini-methode door de algemene formule voor te stellen: r = 58,7265 "tan (z - 1,6081r). |
| |
| Laplace en vervolgens Biot (1828) geven uiteindelijk de volledige (redelijk complexe) theorie van het fenomeen. |
|
|
|
|
|
|