Regenbogen

De regenboog geniet van de optische verschijnselen die in de atmosfeer waargenomen kunnen worden, de grootste bekendheid. Met het zoeken
naar een verklaring hebben vele geleerden en onderzoekers zich eeuwenlang bezig gehouden. Terugkaatsing en breking van licht spelen bij de
vorming een belangrijke rol. Voor een volledige verklaring van het verschijnsel moet men tevens interferentie en buiging, een gevolg van het golfkarakter van licht, erbij betrekken.

Regenboog, Costa Rica.

Bui en regenboog, De Bilt.

Regenboog, station Arnhem.

Van de optische verschijnselen die in de atmosfeer kunnen worden waargenomen, geniet de regenboog de grootste bekendheid. Van oudsher
maakt hij een geweldige indruk op degenen die hem opmerken. De oudst bekende beschrijvingen van de boog komen voor in vroeg Sumerische
en Chaldese verhalen. In de Bijbel wordt de boog voor het eerst genoemd in het verhaal van de zondvloed (Gen. 9.13). In de Griekse mythologie
is de godin Iris de personificatie van de regenboog. Ook andere volken associëren de boog met goddelijke zaken of voorstellingen en in veel
legenden komt hij voor. Afwisselend wordt er een positieve en negatieve betekenis aan gehecht.

Dichters, schilders en geleerden vonden in de regenboog een gezamenlijke bron van inspiratie. De visie van de kunstenaar komt niet altijd overeen met die van de wetenschapsman, die de regenboog probeert te verklaren. Maar ook degenen die een verklaring zochten voor de regenboog waren het dikwijls onderling oneens. Meerdere malen in het verleden dacht men de definitieve verklaring gevonden te hebben; ten onrechte, naar later
bleek, omdat het laatste woord erover nog niet gesproken was en is. Een van de fouten die gemaakt werd, was dat een zo groot vertrouwen
werd gesteld in de als volledig beschouwde theorie, dat controle ervan door middel van waarnemingen werd nagelaten. Omdat de regenboog vaker wordt opgemerkt dan waargenomen, volgt hier een beschrijving van dit prachtige natuurverschijnsel.

Dubbele regenboog (de tweede boog is vaag zichtbaar buiten de eerste). Binnen de eerste boog zijn overtallige regenbogen te zien. Onderaan is
nog net de schaduw van de fotograaf te zien; de schaduw van de camera is het middelpunt van de cirkelboog. Opname in Wrangell-St. Elias
National Park, Alaska.

De regenboog, gezien vanaf de grond. De bij de vorming van de boog betrokken lichtstralen liggen alle op een kegeloppervlak met een tophoek
van 42 graden bij de waarnemer en als as de lijn door de waarnemer en het tegenpunt van de zon

De regenboog

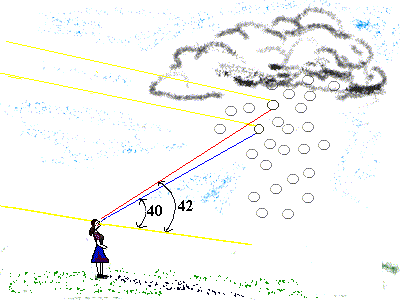
Een regenboog nemen we gewoonlijk alleen dan waar wanneer we, met de rug naar de zon, kijken naar een wolk waaruit regen valt die door
zonlicht wordt beschenen. Het meest opvallend is de zogenoemde hoofdregenboog met een straal van ca. 42° en het tegenpunt van de zon als middelpunt. Van de cirkel zien we meestal slechts een klein gedeelte, enerzijds omdat zich niet overal regendruppels bevinden, anderzijds doordat aardoppervlak en/of bebouwing ons het zicht op de boog verhinderen. Vanuit ballonnen en vliegtuigen is de complete cirkel wel waargenomen.
Buiten de hoofdregenboog is dikwijls een tweede bredere en lichtzwakkere boog, de bijregenboog, zichtbaar. Het middelpunt is weer het tegenpunt van de zon, de straal bedraagt nu ca. 51°. Tussen de bogen ziet de hemel er vaak donkerder uit dan binnen de hoofdboog of buiten de bijboog.

De kleurrijkdom van de regenboog bestaat uit de spectrale kleuren, in meerdere of mindere mate onderling vermengd. Bij de hoofdregenboog
bevindt zich het rood aan de bolle buitenzijde, het violet aan de holle binnenzijde. De kleurenvolgorde van de bijregenboog is juist andersom,
zodat de bogen hun rode kanten naar elkaar toekeren. De lichtsterkte van de boog is gewoonlijk het grootst aan de voet. De begrenzing is
aan de rode kant van de beide bogen scherper dan aan de violette kant. Dikwijls kunnen binnen het violet nog zgn. overtallige bogen worden waargenomen. Ze zijn het duidelijkst zichtbaar bij het hoogste punt van de regenboog en worden vaak sterker tegen het einde van de bui.
In de kleuren van de overtallige bogen overheerst gewoonlijk het rose, groen en violet. In zeldzame gevallen kan men ook bij de bijregenboog overtallige bogen waarnemen.

Afbeelding-1

Afbeelding-2

Afbeelding-3

1: De regenboog, gezien vanuit de lucht. In tegenstelling tot de regenboog gezien vanaf de grond, kan vanuit bijvoorbeeld vliegtuigen een
complete cirkel worden waargenomen. Het zonlicht komt van links boven; als de middelste stippellijn verder naar rechtsonder wordt
doorgetrokken, komt hij uiteindelijk uit in het tegenpunt van de zon

2: Hoofdregenboog vanuit een vliegtuig. We zien de onderste helft van een kleurencirkel. Buiten de boog is de hemel donkerder dan aan
de binnenzijde.Foto: Maaike Floor.

3: Wanneer licht invalt op een grensvlak tussen lucht en water wordt een gedeelte van het licht terug- gekaatst, een ander gedeelte gebroken.
Violet licht wordt sterker gebroken dan rood licht.

Twee regenbogen zijn zelden precies gelijk. Verschillen kunnen optreden in de straal van de rode buitenrand van de boog, de breedte van de boog
en de mate waarin de verschillende kleuren en de overtallige bogen vertegenwoordigd zijn. Ook tijdens een bui kan het aanzien van de boog die
we waarnemen veranderen. Gewoonlijk zijn regendruppels voor de vorming ervan noodzakelijk, hoewel bij andere waterdruppels, zoals van tuinsproeiers, fonteinen, watervallen en opspattend water, het verschijnsel ook te zien is. In mist of bewolking wordt soms wel en boog waargenomen, de mistboog of wolkenboog. De straal is meestal kleiner dan van de gewone regenboog; het verschil kan oplopen tot 8°!
Het licht van de regenboog is steeds gepolariseerd. Dit blijkt als we de boog bekijken door een polaroid zonnebril in verschillende standen.
We zien dan dat er een stand is waarbij hij nagenoeg verdwenen is

Dubbele regenboog Bron: bronlicht.files.wordpress

Afbeelding-5

5: Dubbele regenboog, gezien vanaf het op ongeveer 2800m hoogte gelegen Whipple Observatorium op Mount Hopkins nabij Amado, Arizona.
Foto: Steve West, Smithsonian-University of Arizona.

De hoofdboog

Bij de natuurkundige verklaring van de regenboog gaat men na op welke manier licht dat invalt op een bolvormige waterdruppel, van richting verandert. Het effect van meerder druppels beschouwt men dan als de som van de effecten op een enkele druppel. Met de terugkaatsings- en brekingswetten uit de geometrische optica (Fig. 3) kunnen de verschillende mogelijkheden berekend worden. In Fig. 4b is de stralengang van de hoofdboog gegeven. De hoek die het licht uiteindelijk maakt met het invallende licht noemt men de deviatie (D). Zij hangt af van de hoek van inval;
het verband is weergegeven in Fig. 5(a). Uit de grafiek blijkt dat de deviatie een minimale waarde heeft van bijna 138° voor een invalshoek van ongeveer 59°. Ook blijkt dat relatief veel licht volgens het minimum wordt afgebogen. Voor lichtstralen met invalshoeken tussen 55° en 65°
neemt de deviatie waarden aan tussen 137°58' en 138°45'. Vergelijken we dit met invalshoeken tussen bijv. 10° en 20°, dan zien we dat de
deviatie nu veel sterker varieert: nl. van 160° tot 170°. Zonlicht dat 138° van richting is veranderd lijkt afkomstig van plaatsen op de hemel
met een afstand van 138° tot de zon of een afstand van 180° -138° = 42° tot het tegenpunt van de zon. Omdat veel licht ongeveer volgens
het minimum wordt afgebogen, zien we een lichtcirkel met een straal van 42° om het tegenpunt van de zon.


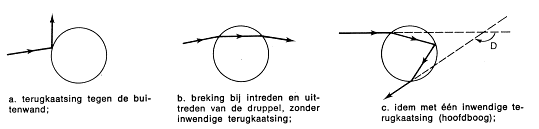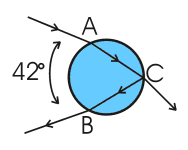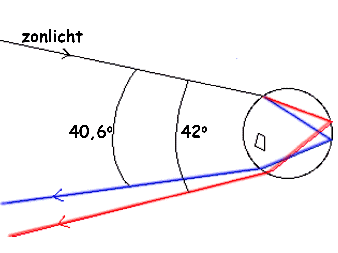
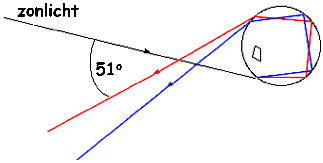Stralengang hoofdregenboog (links) en bijregenboog (boven) met kleurschifting.

Kleurschifting

In het voorgaande is uitgegaan van (monochromatisch) oranje licht, waarvoor de brekingsindex van water gesteld kan worden op 4/3. Zonlicht
bevat echter licht van allerlei kleuren. De brekingsindex van water hangt af van de kleur van het opvallende licht. De berekeningen moeten dus eigenlijk voor alle kleuren afzonderlijk uitgevoerd worden. De kleinste waarde van de brekingsindex geldt voor rood licht; de bijbehorende
deviatie D, is eveneens het kleinst. De straal van de rode boog (180-D) is daardoor het grootst, zodat het rood aan de buitenzijde van de boog wordt waargenomen. Daarbinnen liggen de andere kleuren met het violet aan de naar het tegenpunt van de zon gekeerde binnenkant van de
boog. De invloed van de brekingsindex op de deviatie en daardoor op de grootte van de straal van de boog blijkt ook uit waarneming van een regenboog tijdens een zeereis bij stormachtig weer in het opspattende schuim van de golven. Door de grotere brekingsindex van zeewater is de straalongeveer 1° kleiner dan die van de tegelijkertijd zichtbare gewone boog (zie foto hieronder midden).

Regenboog, Skogafoss (IJsland).

Surfer en regenboog. Foto: Mila Zinkova

Regenboog in zeewater. Foto: NN

Afbeelding-6

Afbeelding-7

6: Gebroken regenboog boven de Pacifische Oceaan ontstaan door regen en door zoutwater van de zee. Foto: J. Dijkema
Bron: Meteorologischer Kalender 2000, Deutsche Meteorologische Gesellschafft, Berlijn.

7: De straal van de regenboog wordt bepaald door de brekingsindex van de waterdruppel. Doordat zout water een andere brekingsindex heft
dan zoet water, is de straal van de regenboog in opspattend zeewater ook anders dan die van de 'gewone' regenboog. Foto: Mila Zinkova.

De bijregenboog

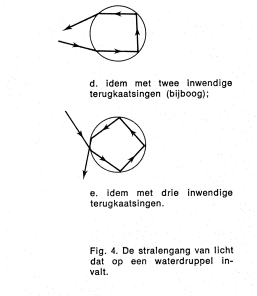
De stralengang van het licht dat de gewone regenboog vormt is niet de enig mogelijke, zoals Fig. 4 al aangaf. Fig. 4c laat het geval zien waarbij
het zonlicht tweemaal wordt teruggekaatst tegen de binnenzijde van de waterdruppel alvorens uit te treden. Lichtstralen die op een dergelijke
manier van richting worden veranderd vormen de bijregenboog. De optredende deviaties kunnen berekend worden op dezelfde manier als bij de hoofdregenboog.

Het resultaat is weergegeven in Fig. 5(b). De minimumdeviatie bedraagt 231°. De verklaring verloopt verder analoog aan die van de hoofd-regenboog. Het tegenpunt van de zon ligt op een afstand van 180° van de zon, de bijregenboog op 231°, zodat de straal 231° -180° = 51° bedraagt. Voor rood licht is de minimumdeviatie weer kleiner, wat in dit geval tot gevolg heeft, dat het rood het dichtst bij het tegenpunt van
de zon wordt waargenomen. De binnenrand van de bijregenboog is daardoor rood van kleur, de buitenrand is violet gekleurd en de kleurvolgorde
is tegengesteld aan die van de hoofdregenboog.

Stralengang van de hoofdregenboog.

Stralengang van de hoofd-regenboog en de bijregenboog.

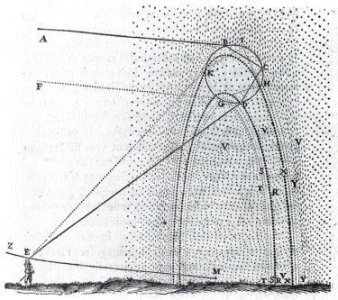Stralengang van de regenboog volgens Descartes, ca 1625.

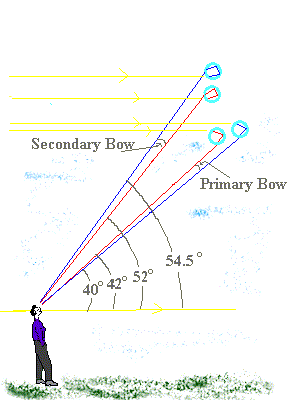
De donkere hemel tussen de bogen

Hoewel de bovenstaande theorie niet volledig is, zoals later zal blijken, kunnen naast de boven beschreven hoofdtrekken van de regenboog
ook nog enkele andere verschijnselen verklaard worden. Op een aantal foto's is te zien, dat de hemel tussen de bogen er donkerder uitziet dan binnen de hoofdregenboog en buiten de bijregenboog. Voor de verklaring gaan we na uit welke richting lichtstralen, die door in de lucht zwevende regendruppels van richting zijn veranderd, afkomstig zijn. Bij de bijregenboog kunnen we de deviatie behalve door de hoek D evenzeer vastleggen
door de hoek a = 360° -D. Het verband tussen a of D en de hoek van inval is uitgezet in Fig. 5(b). Uit de totale figuur blijkt, dat deviaties tussen
129° en 138° niet voorkomen.

Dit betekent, dat geen van de lichtstralen, die de druppels doorlopen op de manier zoals is geschetst in Fig. 4b (één inwendige terugkaatsing: hoofdboog) of Fig. 4c (twee inwendige terugkaatsingen: bijregenboog), afkomstig lijkt uit het gebied tussen de beide regenbogen in, zodat de
hemel er daar donkerder uitziet.

Hoofdregenboog, bijregenboog en donkere band
van Alexander. Foto: NN.

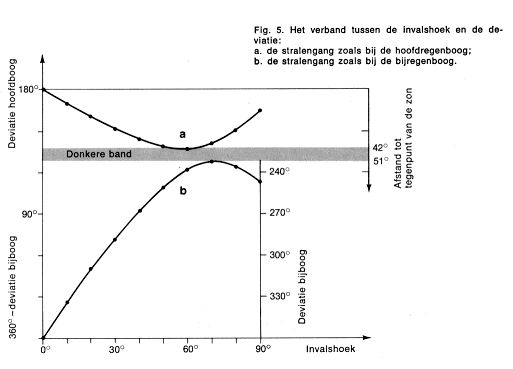Figuur 5. Het verband tussen de invalshoek en de deviatie voor
a) de hoofdregenboog en b) de bijregenboog. Bekijk ook deze animatie

Hoe ver staat de regenboog weg?

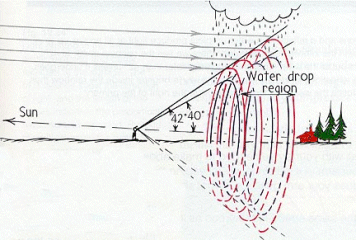
De boog wordt gevormd door licht, dat door regendruppels van richting wordt veranderd. Alle druppels die door de zon beschenen worden en
zich vanuit de waarnemer bezien in een geschikte richting bevinden dragen eraan bij. Ze bevinden zich op afstanden van de waarnemer variërend
van enkele meters tot verscheidene kilometers. De bij de vorming van de boog betrokken (oranje) lichtstralen liggen dus alle op een kegeloppervlak met een tophoek van 42° (resp. 51°) bij de waarnemer en als as de lijn door de waarnemer en het tegen- punt van de zon. Dit verklaart ook,
dat twee waarnemers nooit dezelfde regenboog kunnen zien, omdat het licht afkomstig is van regendruppels op verschillende kegeloppervlakken.
We kunnen dit gewaar worden wanneer we vanuit een rijdende trein een regenboog waarnemen. De boog blijft dan niet vast staan t.o.v. bepaalde herkenningspunten in het landschap, maar reist met ons mee op dezelfde manier als onze schaduw met ons meereist.

Figuur-6

Afbeelding-8

Afbeelding-9

6: Alle druppels die door de zon worden beschenen werken mee aan de vorming van een regenboog. De regenboogcirkels liggen op een kegel.

8: De regenboog is achter de duinen, dus ver weg.

9: De regenboog in het water van een beregeningsinstallatie is vlakbij

Afbeelding-10

Afbeelding-11

Afbeelding-12

10: Regenboog bij weerspiegelde zon, Ameland 14 december 2005. Foto: Martha Appelman

11: Regenbogen, regenbogen bij weerspiegelde zon en weerspiegelde regenboog. Foto: Terje O. Nordvik

12: Regenboog bij weerspiegelde zon in de buurt van Spitsbergen. De horizon loopt door het snijpunt van de bogen. Foto: Nicola Boll.

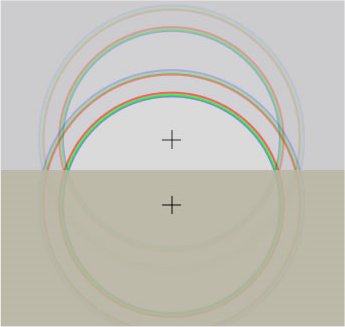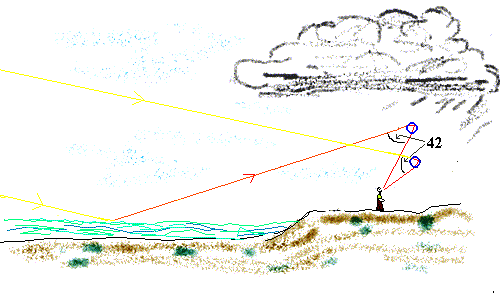
Figuur 7: Regenboog bij weerspiegelde zon.
Bron: Clara/sundog.

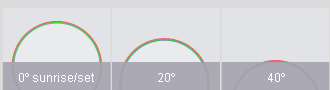
Regenboog bij hoge en lage zonnestanden.

Figuur 8: De stralengang van de regenboog en van de bij weerspiegelde zon.

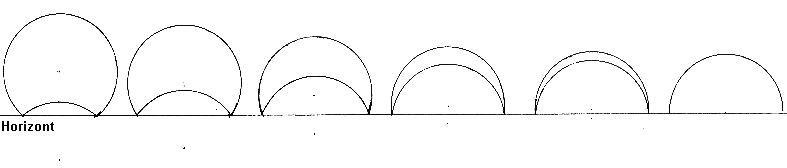Regenboog (onder) en regenboog bij weerspiegelde zon (boven) bij van links af toenemende zonshoogte Bron: Meteoros.

De regenboog bij hoge en lage zonnestanden

's Zomers rond het middaguur wordt nooit een regenboog waargenomen. De verklaring hiervan volgt ook uit de voorgaande theorie. Wanneer
de zonshoogte meer dan 42° bedraagt bevindt het tegenpunt van de zon zich meer dan 42° onder de horizon, zodat de regenboog in zijn geheel onder de horizon verdwijnt. Tot een zonshoogte van ongeveer 52° bevindt zich een gedeelte van de bijregenboog boven de horizon, maar deze lichtzwakke boog wordt minder gemakkelijk opgemerkt wanneer we niet door het zien van de hoofdboog worden gestimuleerd om naar de bijregenboog uit te kijken. Vlak voor zonsondergang wordt soms een rode regenboog waargenomen (zie foto hieronder rechts). Door verstrooiing van het zonlicht in de atmosfeer, die voor korte golflengten (violet) sterker is dan voor lange (rood), overheerst rond deze tijd het rode licht sterk. De regenboog, die beschouwd kan worden als een door regendruppels ontworpen spectrum van de zon, verandert bij zonsondergang van een kleurrijke in een rode boog.

Een lage zonnestand geeft een
hoge regenboog.

Een hogere zonnestand geeft een
lagere regenboog

Vlak voor zonsondergang wordt soms een
rode regenboog waargenomen.

Polarisatie

In het voorgaande hebben we bij de verklaring van de regenboog alleen gelet op het verband tussen de invalshoek en de bijbehorende deviatie,
zoals weergegeven in Fig. 5. Daar waar de deviatie het minst verandert voor een kleine verandering van de hoek van inval verwachten we de grootste lichtsterkte. Geen rekening is gehouden met de afname van de lichtsterkte, die bij elke breking of terugkaatsing optreedt. Hoe deze
afname plaatsvindt kan nagegaan worden door licht op te vatten als een transversale trilling. De trillingsrichting staat loodrecht op de richting
waarin het licht zich voortplant. Indien overigens geen voorkeursrichting aanwezig is spreekt men van ongepolariseerd licht. Men kan dit
samengesteld denken uit licht met trillingsrichtingen resp. evenwijdig aan, en loodrecht op het vlak van inval. Van ongepolariseerd licht zijn de
beide componenten even groot. Door terugkaatsing en breking kunnen echter voorkeursrichtingen voor de trilling ontstaan. Daardoor wordt het teruggekaatste en gebroken licht in meerdere of mindere mate gepolariseerd en nemen de genoemde componenten verschillende waarden aan.
De werking van polaroid zonnebrillen berust op de .polarisatie van het teruggekaatste zonlicht, waardoor deze brillen ongewenste reflecties van zonlicht verzwakken.

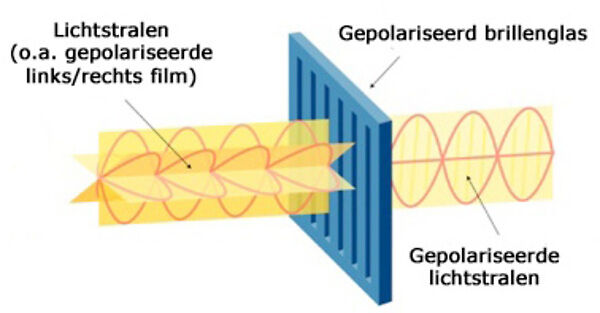Werking van een gepolariseerd brillenglas

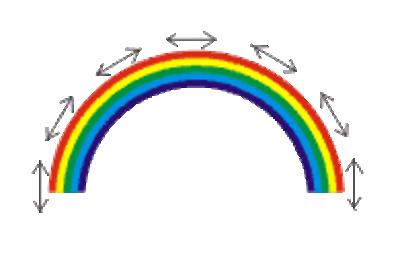De richting van de polarisatie van de regenboog.

Bovenstaande foto's werden vlak na elkaar gemaakt. Alleen de stand van het
polarisatie-filter was anders. Foto: nandoonline fotografie

Een derde boog?

De stralengang waardoor de bijregenboog gevormd wordt, verschilt slechts in één opzicht van die van de hoofdregenboog: het aantal inwendige terugkaatsingen. Vandaar dat de gedachte aan een derde regenboog voor de hand ligt; deze zou gevormd moeten worden door licht dat niet één (hoofd-) of twee (bijregenboog) maar drie inwendige terugkaatsingen ondergaat alvorens uit te treden (Fig. 4d). Een dergelijke regenboog is nooit aan de hemel waargenomen. Met de brekingswetten is wel de plaats te berekenen waar naar de boog gezocht moet worden.

De optredende minimumdeviatie bedraagt ca. 318°, zodat de derde boog als een kring om de zon met een straal van 42° zou moeten verschijnen. Door de derde terugkaatsing is de lichtsterkte echter nog geringer dan die van de niet altijd waarneembare bijregenboog. En omdat in de richting
van de zon gekeken moet worden, zal het lichtzwakke verschijnsel gewoonlijk tegen een heldere achtergrond bekeken moeten worden, wat het waarnemen erg moeilijk maakt. Desondanks zou men onder bijzonder gunstige omstandigheden (bijv. door de hand voor de zon te houden en
met een donkere wolkenlucht als achtergrond), in zeldzame gevallen op het zichtbaar worden van de derde boog kun- nen hopen. Dat dit echter
zeer onwaarschijnlijk is blijkt, behalve uit het feit dat de boog nooit werd waargenomen, uit berekeningen m.b.v. fresnelcoëfficiënten waarin de lichtsterkte van regenbogen (stralengang volgens Fig. 4b, c, d) wordt vergeleken met die van door dezelfde druppels in dezelfde richting teruggekaatst licht (stralengang volgens Pig. 4a).

Bij de hoofdboog bedraagt de lichtsterkte van het weerkaatste licht minder dan die van het licht dat de boog vormt; bij de bijregenboog vinden
we dezelfde orde van grootte maar een derde boog wordt volledig overstraald door het weerkaatste licht. Derde en hogere orde bogen kunnen
wel worden waargenomen onder laboratoriumomstandigheden. De verzwakking van het licht waarvan bij drie inwendige terugkaatsingen sprake
is, speelt een ondergeschikte rol bij licht dat zonder inwendige terugkaatsingen de druppel weer verlaat (Fig. 4b). Ook hier zouden we een derde regenboog kunnen verwachten, omdat het licht, evenals bij de hoofd- en de bijregenboog, tweemaal gebroken is. Desondanks vormt zich op
deze manier geen regenboog. In dit geval varieert de deviatie tussen 0° en 84°, waarbij de lichtsterkte afneemt bij toenemende deviatie.
Door overlap van de kleuren is het licht wit, op een violette rand na, die echter veel te lichtzwak is om te worden waargenomen.

Figuur-9

Figuur-10

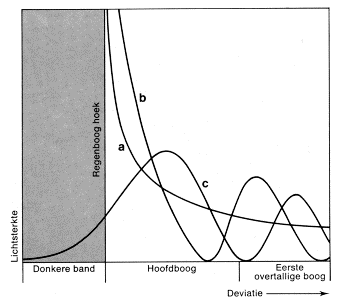
9. Het verband tussen de lichtsterkte en de deviatie: a. v1olgens de geometrische optica (Descartes); b. rekening houdend met interferentie
(Young); c. rekening houdend met buiging (Airy). Regenbooghoek: minimum deviatie en hoek waarbij de grootste licht- sterkte optreedt
volgens de geo- metrische optica (voor oranje ca. 138°)

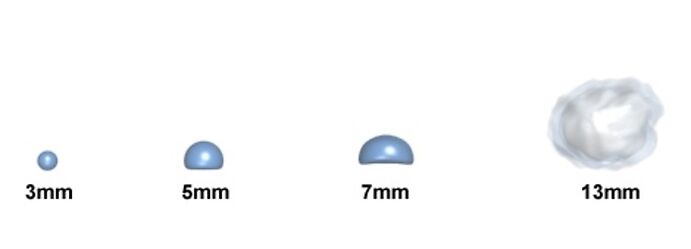
10. Afplatting van regendruppels van verschillen- de diameter; hoe groter de diameter, des te sterker de afplatting.

Interferentie

Indien regenbogen zich uitsluitend vormden volgens de theorie zoals die hier is geschetst, zouden twee regenbogen op elkaar lijken als twee
druppels water. De grenzen van de boog zouden worden bepaald door de brekingsindices van rooden violet licht. Uit de stralengang voor rood
(41°20') en violet licht (40°24') kan de (constante) breedte van een dergelijke boog worden bepaald. Brengt men het feit in rekening dat de zon geen puntvormige lichtbron is, dan zou de breedte van de boog steeds 2°28' bedragen. Overtallige bogen zouden afwezig zijn en mistbogen
zouden even kleurrijk en even groot zijn als gewone regenbogen. Bovendien zou de overgang van het rood van de regenbogen naar het donkere gebied tussen de beide bogen zeer abrupt verlopen, waardoor de donkere band altijd duidelijk waarneembaar zou zijn.

Vergelijken we de gegeven beschrijving van de regenboog hiermee, dan kunnen we concluderen dat de verklaring van de boog nog andere
elementen dan de genoemde moet be- vatten. Het blijkt noodzakelijk interferentie en buiging, beide een gevolg van het golfkarakter van licht,
in een theorie over de regenboog te betrekken. Interferentie is het verschijnsel dat lichtgolven elkaar kunnen versterken of uitdoven op dezelfde manier als dat bij watergolven gebeurt: twee golftoppen geven een dubbelgrote uitwijking (versterking), een golftop en een golfdal resulteren in
een uitwijking nul (uitdoving). Dat interferentie een rol speelt is als volgt in te zien. Uit Fig. 5 blijkt dat een deviatie van bijv. 150° optreedt bij
twee invalshoeken. Met andere woorden: lichtstralen die 150° van richting worden veranderd kunnen twee verschillende wegen afleggen door
de regendruppel.

Het licht dat de langste weg aflegt loopt echter achter op het overige licht. Op deze manier ontstaan onderlinge faseverschillen tussen de
lichtstralen die een waarnemer vanuit dezelfde richting bereiken. Afhankelijk van de grootte van het faseverschil treedt versterking of uitdoving
op. Voor lichtstralen die minimaal worden afgebogen zal het verschil in weglengte zeer gering zijn; zij versterken elkaar. Pas bij grotere deviaties
oopt het weglengteverschil op tot een halve golflengte, waarbij uitdoving optreedt. Neemt de deviatie nog meer toe, dan zal weer versterking optreden, enz. Het resultaat is een aantal opeenvolgende lichte en donkere banden.

In Fig. 9(b) is dat weergegeven voor licht van een bepaalde golflengte (kleur). Voor andere golflengten ontstaat een vergelijkbaar patroon,
waarvan pieken en dalen op andere plaatsen liggen. De regenboogis de som van de bogen voor de verschillende kleuren afzonderlijk.
Is bijvoorbeeld de lichtsterkte voor rood maximaal bij afwezigheid van licht van andere kleuren, dan treffen we op die plaats rood aan;
zijn ook andere kleuren aanwezig, dan ontstaat een mengkleur.

Kleureffecten bij interferentie van lichtgolven
in een zeepvlies.

Regenboog te Katwijk met overtallige bogen.
Foto's: Theo Westra

Regenboog te Katwijk met overtallige bogen.
Foto's: Theo Westra .

Buiging

Met behulp van interferentie is het voorkomen van overtallige bogen aannemelijk te maken. De wisselende stralen en breedten van de bogen
van een bepaalde kleur vormen echter nog een probleem. Ook de abrupte overgang van de regenboog naar het donkere gebied tussen de bogen
is onwaarschijnlijk, gezien het golfkarakter van licht. Wanneer lichtbundels gedeeltelijk onderbroken worden door obstakels treden geen scherpe schaduwgrenzen op. Enerzijds blijkt het licht zich enigszins om het obstakel heen te buigen, waardoor toch nog wat licht valt op plaatsen waar
we bij rechtlijnige voortplanting van het licht schaduw zouden verwachten. Anderzijds vinden we lichte en donkere banden op plaatsen waar het obstakel bij een rechtlijnige stralengang geen invloed meer uit zou oefenen. Het golfkarakter van licht, dat voor deze verschijnselen bij obstakels in een lichtweg verantwoordelijk is, maakt eveneens de bovengenoemde overgang aan de rode rand van de regenboog minder abrupt. Ook hier blijkt door buiging toch nog wat licht in het donkere gebied terecht te komen en treden donkere en lichte banden op in het lichte gedeelte.

De lichtsterkteverdeling, zoals die in Fig. 9 is weergegeven, werd gevonden door Airy en later door anderen verder uitgewerkt. We zien dat de grootste lichtsterkte niet wordt gevonden voor de met de brekingswetten bepaalde minimumdeviatie: de straal van de regenboog krijgt een
kleinere waarde. Uit lichtsterkteberekeningen volgens de buigingstheorie bleek verder het belang van de grootte van de betrokken regendruppels. Voor kleinere druppels treden eerder overtallige bogen op, neemt de straal van de regenboog af, de breedte toe en krijgt hij door vermenging
van spectrale kleuren een fletser of witter aanzien. Op grond van de buigingstheorie kan men ook overtallige bogen verwachten aan de buitenzijde van de bijregenboog. Door de grotere breedte van deze boog wordt het verschijnsel minder uitgeproken, lichtzwakker en minder kleurrijk.
De buigingstheorie verklaart ook de mistboog, wolkenboog ofwitte regenboog, waarin nauwelijks enige kleur waarneembaar is en waarvan
de straal soms 8° minder bedraagt dan volgens de geometrische optica verwacht mag worden. De mistboog moet men niet verwarren met
de regenboog, zoals die in zeldzame gevallen bij maanlicht kan worden waargenomen. Beide vertonen weinig kleur en maken een witte indruk.
Bij de maanregenboog wordt dat echter veroorzaakt door de geringe lichtsterkte van het maanlicht. Bij kleine lichtintensiteiten is ons oog minder gevoelig voor kleur dan bij grotere, zodat de oorzaak van de afwezigheid van kleur in het oog schuilt en niet in de ontstaanswijze.

Wolkenboog. Foto: Peter de Vries.

Verdere verfijningen van de theorie

Met de buigingstheorie van Airy werd de verklaring van de regenboog vollediger. De invloed van de grootte van de druppels was onderkend,
zodat aan een verdere uitwerking begonnen kon worden. Zo werd onderzocht hoe de regenboog verandert wanneer van een grootteverdeling
van de regendruppels wordt uitgegaan, zoals die ook onder regenwolken wordt aangetroffen. Onder dergelijke omstandigheden worden de
overtallige bogen minder uitgesproken of verdwijnen ze zelfs geheel. Wanneer men de afmetingen van de zonneschijf, die als lichtbron fungeert,
in de berekeningen betrekt, verliezen de overtallige bogen eveneens een gedeelte van hun kleur. Het effect is het grootst als de zon door een
mist of nevel heen schijnt, waardoor de werkzame doorsnede van de lichtbron groter wordt. Bij mistbogen is dit meestal het geval, zodat de
kleuren vlakker zijn zowel door de kleine afmetingen van de druppels als door de grotere werkzame doorsnede van de lichtbron.

Regenboog in plantenspuit

Regenboog in sproei-installatie, Egond

Regenboog in fontein, Zwolle.

Onregelmatigheden

Behalve onderlinge verschillen tussen waargenomen regenbogen, komen er ook onregelmatigheden voor die aan één en dezelfde boog kunnen worden opgemerkt. Het betreft hier de overtallige bogen, die aan het hoogste punt duidelijker zichtbaar zijn dan in het verticale gedeelte van de
boog, waar de lichtintensiteit het grootst en de rode kleur het zuiverst is. Voor een mogelijke verklaring hiervan zou men kunnen denken aan een geleidelijke toename in grootte van de regendruppels tijdens hun val naar het aardoppervlak. Bij grote druppels liggen de overtallige bogen namelijk
zo dicht bij elkaar, dat ze vervagen door overlap van de verschillende kleuren en door de grootte van de zonneschijf. Tegen deze verklaring pleit de constante afstand van de overtallige bogen tot de hoofdboog, die in de meeste gevallen wordt waargenomen. Zouden de druppels geleidelijk groter worden, dan zou die afstand moeten afnemen met afnemende hoogte. Bovendien zou de rode band onder het verticale gedeelte van de boog,
soms waarneembaar vanaf een bergtop, lichtsterker moeten worden als de druppels bij het vallen steeds groter werden. Bij waarnemingen bleek
dit niet het geval te zijn.

De verklaring voor de genoemde onregelmatigheden moet veeleer gezocht worden in afwijkingen van de bolvorm bij grotere regendruppels
(zie Fig. 10). Kleine druppels (kleiner dan ca. 0,5 mm) zijn gewoonlijk bolvormig, omdat als gevolg van de oppervlaktespanning het oppervlak
van een vrije hoeveelheid vloeistof een zo klein mogelijke afmeting aan zal nemen. Onder invloed van de luchtweerstand worden de grotere
druppels afgeplat, vooral aan de onderkant. Het gevolg is dat de doorsnede van de druppel met het vlak waarin de lichtstralen lopen niet meer cirkelvormig is bij verticale doorsneden maar wel bij ongeveer horizontale doorsneden. De doorsnede is horizontaal in het verticale gedeelte van
de boog, zodat daar de grotere druppels op normale wijze aan het tot stand komen van de regenboog mee kunnen werken. Bevinden de
lichtstralen zich in een ander vlak, hetgeen bijv. in het hoogste punt van de regenboog het geval is, dan doorloopt het licht afgeplatte druppels, waardoor de straal van de bijbehorende regenboog afneemt. Hoeveel deze kleiner wordt hangt af van de mate van vervorming, dus van de druppelgrootte. Omdat de druppels van verschillende grootte naast eIkaar voorkomen, resulteert er geen gezamenlijke bijdrage, waardoor de regenboog uitsluitend door de kleinere druppels wordt gevormd. In dat gedeelte van de boog kunnen we dus een geringere lichtintensiteit van de maxima verwachten en eigenschappen die horen bij een door kleine druppels gevormde boog: minder rood en duidelijke, overtallige bogen.

Een andere onregelmatigheid aan regenbogen is waargenomen tijdens onweersbuien. Bij iedere donderslag leek de boog te trillen, hetgeen vooral zichtbaar was aan de voor kleine veranderingen van de druppels gevoelige overtallige bogen. De oorzaak ligt vermoedelijk in trillingen van regendruppels die door de geluidsgolven van de donder worden opgewekt. Onregelmatigheden treden ook op wanneer het 'regengordijn' waarin de boog wordt waargenomen niet overal dezelfde druppelgrootteverdeling heeft. Dit kan bijvoorbeeld gebeuren wanneer meerdere buien bij de vorming van het gordijn betrokken zijn. Onregelmatigheden in de overtallige bogen en zelfs 'knikken' in de regenboog kunnen hiervan het gevolg zijn.

Geschiedenis

De verklaring van de regenboog blijkt een groot aantal wetenschappers in het verleden te hebben bezig gehouden. Het begin van de theorie
vorming bij de overgang van mythologie naar natuurwetenschap is moeilijk aan te geven. De eerste niet-mythologische uitspraken over de regenboog vinden we bij leden van de zogenoemde Ionische school, waarvan Thales van Milete (ca. 600 v. Chr.) leider was. Zijn leerling
Anaximenes (ca. 575 v. Chr.) wees op het verband tussen de regenboog en het zichtbaar zijn van de zon. Van de geleerden uit de tijd van de
Griekse beschaving drukte - zoals ook op vele andere terreinen - Aristoteles (ca. 350 v. Chr.) het grootste stempel op de ideeën die als verklaring voor de regenboog gangbaar werden. Hij ging er vanuit dat de boog wordt gevormd als zonlicht op een donkere wolk valt en wordt teruggekaatst naar het oog van een waarnemer. Deze opvattingen bracht hij niet als eerste, maar hij gaf ze wel het gewicht van zijn autoriteit, waardoor ze ruim duizend jaar lang nauwelijks weersproken werden. Bij Aristoteles vinden we ook de oudste beschrijving van de bijregenboog. Het aantal kleuren van de boog stelde hij op drie: rood, groen en violet. De overige kleuren schreef hij toe aan menging of contrast. De donkere hemel tussen de bogen werd het eerst opgemerkt door Alexander van Aphrodisias (ca. 200 n. Chr.).

Ook in de Middeleeuwen zat men sterk vast aan terugkaatsing van lichtstralen tegen wolken of schermen die zich tussen wolk en waarnemer
zouden bevinden. Omstreeks 1225 gebruikte Robert Grosseteste breking van licht bij de verklaring van de regenboog. Zijn leerling Robert Bacon
(ca. 1250) gaf als eerste een schatting van de straal van de boog. De opgegeven waarde van 42° is opvallend nauwkeurig. Door de doorsnede
van de kleine kring (een halo) eveneens te schatten op 42° (nu houdt men hiervoor 44° aan) bracht hij latere onderzoekers in verwarring:
er werd een verband tussen de kleine kring en de regenboog gesuggereerd, dat in werkelijkheid niet bestaat.

Een grote stap voorwaarts vormden de ideeën van Theodoricus (Dietrich) van Freiberg (ca. 1300). Hij beschouwde een bol met water als een vergrote regendruppel, dus niet als een verkleinde bolvormige wolk. Daaraan koppelde hij de gedachte dat de regenboog de som van de effecten
is van alle druppels afzonderlijk. Op grond van de experimenten die hij uitvoerde, kwam hij tot de conclusie dat de regenboog wordt veroorzaakt
door lichtstralen die een weg afleggen met twee brekingen en een terugkaatsing, zoals aangegeven in fig. 3c. Ongeveer tegelijkertijd presenteerde
de Perzische geleerde Kamal al-Din al-Farisi een vergelijkbare regenboogtheorie. Vermoedelijk werkte hij echter de ideeën uit van zijn leermeester Qutb al-Din al-Shirazi, die naar men aanneemt als eerste interne terugkaatsing en breking van zonlicht door waterdruppels in dé lucht gebruikte
om de regenboog te verklaren. Kamal ging, evenals Theodoricus, systematisch na welke weg het licht volgt in een bol van water. Als eerste nam
hij waar dat er ook lichtstralen uittraden na driemaal inwendig te zijn teruggekaatst. Een derde boog aan de hemel achtte hij echter onmogelijk.

De theorieën van Qutb al-Din en Theodoricus werden in hun tijd en de eeuwen daarna geen gemeengoed. Verdere kwantitatieve uitwerking werd
pas mogelijk nadat de brekingswet uit de geometrische optica, die wordt toegeschreven aan onze landgenoot Willebrord Snel van Royen
(ca. 1600) bekend was. Descartes (ca. 1625) formuleerde de wet in de vorm zoals die ook nu nog gebruikelijk is (sin i = nsin r) en berekende nauwgezet de gang van 1000 lichtstralen die op verschillende plaatsen op een bol van water invallen. Uit zijn berekeningen concludeerde hij dat
er bij één inwendige terugkaatsing veel meer lichtstralen zichtbaar zijn onder een hoek van 41°-42° dan onder elke andere kleinere hoek; onder grotere hoeken zijn geen lichtstralen zichtbaar. Voor de bijregenboog kwam hij tot een vergelijkbaar resultaat. Descartes herontdekte dus niet
alleen de theorie uit het begin van de 14e eeuw, maar gaf deze tevens een steviger ondergrond door de goede overeenkomst tussen
waargenomen en berekende waarden. Verklaring van de kleuren van de regenboog werd pas mogelijk nadat onder anderen Newton in 1666 had aangetoond dat wit licht bestaat uit en ontleed kan worden in licht van verschillende kleuren en dat de mate van breking afhankelijk is van de kleur van het licht. Het aantal kleuren van de boog stelde hij op 7: rood, oranje, geel, groen, blauw, indigo en violet.

Met de theorieën van Descartes en Newton leek alles over de regenboog gezegd te zijn of gezegd te kunnen worden. Zo berekende de Engelse astronoom Hally (ca. 1700) de plaats van de derde regenboog en vond dat het een cirkel om de zon moest zijn met een straal van ongeveer
42°. Men bleek meer dan 2000 jaar lang op de verkeerde plaats aan de hemel naar een eventuele derde boog te hebben gezocht! Geen verklaring gaf de theorie echter voor de reeds in de 13e eeuw door Witelo en later door Theodoricus beschreven overtallige bogen. De Engelse fysicus Young (ca. 1800), die het golfkarakter van licht aantoonde d.m.v. interferentie, gaf met interferentie tevens een verklaring voor de overtallige bogen. De experimenten van Brewster (ca. 1815) met betrekking tot polarisatie van teruggekaatst licht, maakten de waargenomen polarisatie van de regenboog begrijpelijk. Ter verklaring van de kleine stralen van waargenomen mistbogen diende de regenboog in verband gebracht te worden met buiging, hetgeen Comparetti in 1787 als eerste deed. Fresnel (ca. 1820) berekende de intensiteit van de buigingsbeelden aan de hand van scherpe schaduwen in het algemeen. Airy spitste dergelijke berekeningen in 1836 toe op de regenboog. De buigingstheorie wordt daarom ook vaak als airytheorie aangeduid. Pernter (ca. 1900) werkte deze theorie nauwgezet uit en vergeleek de resultaten met waargenomen regenbogen.

Sinds de verklaring van de regenboog volgens Airy is een gedegen wiskundige kennis noodzakelijk om de theorie over de regenboog volledig af
te leiden. Daarom zal deze theorie zelden in opticaleerboeken of schoolboeken worden aangetroffen. In deze eeuw is de rol van de wiskunde
nog groter geworden. Bij de ontwikkeling van de theorie probeert men de verstrooiing van licht aan waterdruppels, die aanleiding geeft tot de regenboog, onder te brengen in een algemenere strooiingstheorie (Mie, Debye, ca. 1919). Daarnaast wordt rekening gehouden met verschillende, naast elkaar voorkomende druppelgrootten, de afwijking van de bolvorm bij grote druppels en de afmetingen van de zonneschijf. Verder komt het deeltjeskarakter van licht meer in de belangstelling te staan bij natuurkundigen. In het verlengde hiervan liggen de moderne uitwerkingen van de regenboogtheorieën. Uitgaande van de overeenkomsten tussen de verstrooiing van deeltjes en van licht tracht men via een algemene theorie tot steeds exactere beschrijvingen van dit prachtige natuurverschijnsel te komen.

Literatuur:
Boyer, C. B., 1959. The rainbow, New York.
Minnaert, M., 1968. De natuurkunde van 't vrije veld I: Licht en kleur in het Landschap, Zutphen, p. 197 e.v.
Nussenzweig, H. M., 1977. The theory of the rainbow, Scientific American, mei 1977, p. 116 e.v.
Tricker, R. A. R., 1970. Introduction to meteorological optics, New York, London, p. 42 e.v. en p. 169 e.v.
Volz, F., 1961. Optik der Tropfen 3: Der Regenbogen, Handb. Geoph. VIII, Berlin, p. 943 e.v.

Bron Kees Floor: Geplaatst in: Natuur en Techniek, december 1977

Categorieën: Optische verschijnselen I Wolkenatlas I Weer A tot Z